题目内容
18. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{25}$ |
分析 根据已知条件得到$\frac{OD}{OC}$=$\frac{1}{5}$,根据相似三角形的判定和性质即可得到结论.
解答 解:∵S△DOE:S△EOC=1:5,
∴$\frac{OD}{OC}$=$\frac{1}{5}$,
∵DE∥AC,
∴△ODE∽△OCA,
∴$\frac{DE}{AC}$=$\frac{OD}{OC}$=$\frac{1}{5}$,
∵DE∥AC,
∴△BDE∽△BAC,
∴$\frac{BE}{BC}=\frac{DE}{AC}$=$\frac{1}{5}$,
∴$\frac{BE}{EC}$=$\frac{1}{4}$,
故选B.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7.把函数y=3x+2的图象沿y轴向下平移一个单位,得到的关系式是( )
| A. | y=3x+1 | B. | y=3x+3 | C. | y=3x-1 | D. | y=3x+5 |
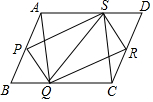 如图,平行四边形PQRS四个顶点恰好分别落在平行四边形ABCD的四条边上,请你判断以A、Q、C、S为顶点的四边形是什么形状,并说明理由.
如图,平行四边形PQRS四个顶点恰好分别落在平行四边形ABCD的四条边上,请你判断以A、Q、C、S为顶点的四边形是什么形状,并说明理由.
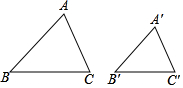 如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗?
如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗?