Question

8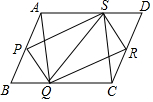．如图，平行四边形PQRS四个顶点恰好分别落在平行四边形ABCD的四条边上，请你判断以A、Q、C、S为顶点的四边形是什么形状，并说明理由．

Answer 1

分析 先连接PR，根据平行四边形的性质，得到PQ=RS，∠BPQ=∠DRS，∠B=∠D，进而判定△BPQ≌△DRS（AAS），即可得到BQ=DS，再根据QC∥AS，可得四边形AQCS是平行四边形．

解答 解：四边形AQCS是平行四边形．
理由：如图，连接PR，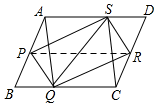

∵四边形PQRS是平行四边形，
∴PQ=RS，PQ∥RS，
∴∠QPR=∠SRP，
∵四边形ABCD是平行四边形，
∴AB∥CD，∠B=∠D，
∴∠BPR=∠DRP，
∴∠BPR-∠QPR=∠DRP-∠SRP，即∠BPQ=∠DRS，
在△BPQ和△DRS中，
$\left\{\begin{array}{l}{∠B=∠D}\\{∠BPQ=∠DRS}\\{PQ=RS}\end{array}\right.$，
∴△BPQ≌△DRS（AAS），
∴BQ=DS，
又∵平行四边形ABCD中，BC=AD，
∴QC=AS，而QC∥AS，
∴四边形AQCS是平行四边形．

点评 本题主要考查了平行四边形的判定与性质的运用，解题时注意：一组对边平行且相等的四边形是平行四边形．