题目内容
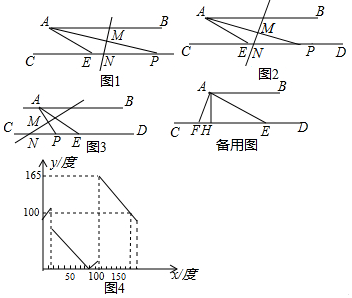
9.如图1,AB∥CD,E是直线CD上的一点,且∠BAE=30°,P是直线CD上的一动点,M是AP的中点,直线MN⊥AP且与CD交于点N,设∠BAP=x°,∠MNE=y°.(1)在图2中,当x=12时,∠MNE=102°;
在图3中,当x=50时,∠MNE=40°;
(2)研究表明:y与x之间关系的图象如图4所示(y不存在时,用空心点表示,请你根据图象直接估计当y=100时,x=10或170.
(3)探究:当x=15或105时,点N与点E重合;
(4)探究:当x>105时,求y与x之间的关系式.
分析 (1)当x=12时,根据三角形外角的性质可:∠MNE=90°+12°=102°;
当x=50°,根据直角三角形两锐角互余可得结论;
(2)由图象直接得出结论;
(3)分两种情况:①P在E的左侧,②P在E的右侧,根据平行线的性质和中垂线的性质可得结论;
(4)如图7,根据三角形外角和为360°列式可得结论.
解答 解:(1)如图2,∵AB∥CD,
∴∠BAP=∠APN=x°,
∵MN⊥AP,
∴∠PMN=90°,
∴∠MNE=∠PMN+∠APN=90°+x°,
当x=12时,∠MNE=(90+12)°=102°;
即y=102°,
如图3中,当x=50时,∠APN=50°,
∴y=∠MNE=90°-x°=90°-50°=40°,
故答案为:102°,40°;
(2)如图2,当0<x<30时,y=90+x,
此时,y=100时,90+x=100,x=10,
由图4可知:y=100时,还有x=170,
∴当y=100时,x=10或170,
故答案为:10或170;
(3)①P在E的左侧时,当N与E重合时,如图5,∠BAE=∠AEP=30°,
∵MN是AP的中垂线,
∴AE=PE,
∴∠AEM=∠PEM=15°,
∴∠EAP=90°-15°=75°,
∴∠BAP=x=30°+75°=105°,
②P在E的右侧时,当N与E重合时,如图6,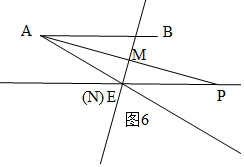
∵AB∥CD,
∴∠BAP=∠APE=x,
同理得:AE=PE,
∴∠EAM=∠EPM=x,
∵∠BAE=30°,
∴∠BAP=x=∠EAP=$\frac{1}{2}∠BAE$=15°,
综上所述,当x=15或105时,点N与点E重合;
故答案为:15或105;
(4)当x>105时,如图7,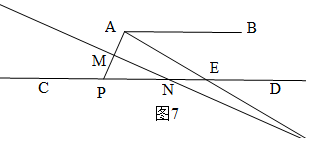
∵AB∥CD,
∴∠APC=∠BAP=x,
∵∠APC+∠MNE+∠AMN=360°,∠AMN=90°,
∴∠APC+∠MNE=360°-90°=270°,
∴∠MNE=270°-∠APC=270°-∠BAP,
即y=270-x.
点评 本题考查了平行线的性质、等腰三角形三线合一的性质、中垂线的性质、三角形外角定理、一次函数,属于动点问题的函数图象,有难度,并采用了分类讨论,数形结合思想解决问题.

 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )| A. | $\frac{125}{12}$ | B. | $\frac{125}{24}$ | C. | 40 | D. | 20 |
 在图中,梯形的个数为( )
在图中,梯形的个数为( )| A. | 6 | B. | 9 | C. | 15 | D. | 27 |
| A. | (x-3)2=8 | B. | (x-3)2=-10 | C. | (x+3)2=8 | D. | (x+3)2=-10 |
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{25}$ |
优惠一:
| 充值金额(元) | 充值后卡内金额(元) | |
| 以前 | 即日起 | |
| 200 | 200 | 250 |
| 500 | 600 | 650 |
| 1000 | 1200 | 1400 |
| 购买服装的标价(元) | 折扣 | |
| 以前 | 即日起 | |
| 1-100 | 不打折 | 不打折 |
| 100-300 | 不打折 | 9折 |
| 300-400 | 9折 | 8折 |
| 不低于400 | 8折 | 7折 |
若该店服装的标价都是正整数,请解决以下问题:
(1)在该店公布好消息的前、后,如果顾客都是充值1000元,在所买服装打折后的价格不超过会员卡内金额的前提下,可买到最贵的服装的标价相差了多少元?
(2)小红和小亮都在该店公布好消息之后办了会员卡,两人各买了一件标价高于300元的服装,小亮所买服装的标价比小红的高,但比较打折后的价格,小亮的低,求小亮买的服装的标价的范围.