学校新年联欢会上某班矩形有奖竞猜活动.猜对问题的同学即可获得一次摇奖机会.摇奖机是一个圆形转盘.被分成16等分.摇中红.黄.蓝色区域.分获一.二.三等奖.奖品分别为台灯.笔记本.签字笔．请问:(1)摇奖一次.获得笔记本的概率是多少?(2)小明答对了问题.可以获得一次摇奖机会.请问小明能获得奖品的概率有多大?请你帮他算算．题目和参考答案——青夏教育精英家教网—

题目内容

7．

学校新年联欢会上某班矩形有奖竞猜活动，猜对问题的同学即可获得一次摇奖机会，摇奖机是一个圆形转盘，被分成16等分，摇中红、黄、蓝色区域，分获一、二、三等奖，奖品分别为台灯、笔记本、签字笔．请问：
（1）摇奖一次，获得笔记本的概率是多少？
（2）小明答对了问题，可以获得一次摇奖机会，请问小明能获得奖品的概率有多大？请你帮他算算．

分析（1）直接利用概率公式求出答案；
（2）首先得出中奖的可能数除以总数，求出答案．

解答解：（1）如图所示：黄色的有2个，则摇奖一次，获得笔记本的概率是：$\frac{2}{16}$=$\frac{1}{8}$；

（2）如图所示：获奖的机会有7个，故一次摇奖，能获得奖品的概率为：$\frac{7}{16}$．

点评此题主要考查了几何概率，正确把握概率公式是解题关键．

练习册系列答案

创维新课堂系列答案

世纪百通主体课堂小学课时同步达标系列答案

18．

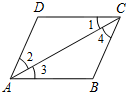如图所示，下列推理及所注理由错误的是（　　）

	A．	∵∠1=∠3，∴AB∥CD（内错角相等，两直线平行）
	B．	∵AB∥CD，∴∠1=∠3（两直线平行，内错角相等）
	C．	∵AD∥BC，∴∠2=∠4（两直线平行，内错角相等）
	D．	∵∠2=∠4，∴AB∥CD（内错角相等，两直线平行）

15．下列说法错误的是（　　）

	A．	必然事件的概率是1
	B．	如果某种游戏活动的中奖率为40%，那么参加这种活动10次必有4次中奖
	C．	了解一批灯泡的使用寿命适合用抽样调查
	D．	数据1、2、2、3的平均数是2

2．