Question

19．△ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．

Answer 1

分析 利用三角形中线的性质、中位线的定义和性质证得四边形EFGD的对边DE∥GF，且DE=GF=$\frac{1}{2}$BC；然后由平行四边形的判定--对边平行且相等的四边形是平行四边形，继而证得结论．

解答 证明：
连接DE，FG，
∵BD、CE是△ABC的中线，
∴D，E是AB，AC边中点，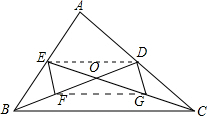
∴DE∥BC，DE=$\frac{1}{2}$BC，
同理：FG∥BC，FG=$\frac{1}{2}$BC，
∴DE∥FG，DE=FG，
∴四边形DEFG是平行四边形，
∴EF∥DG，EF=DG．

点评 本题考查了三角形中位线定理、平行四边形的判定．平行四边形的判定：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；一组对边平行，一组对角相等的四边形是平行四边形