题目内容
17.先化简,再求值:$({\frac{1}{x-y}+\frac{2}{{{x^2}-xy}}})÷\frac{x+2}{2x}$,其中实数x、y满足$y=\sqrt{x-2}-\sqrt{4-2x}+1$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,根据负数没有平方根求出x与y的值,代入计算即可求出值.
解答 解:原式=$\frac{x+2}{x(x-y)}$•$\frac{2x}{x+2}$=$\frac{2}{x-y}$,
∵y=$\sqrt{x-2}$-$\sqrt{2(2-x)}$+1,
∴x-2≥0,2-x≥0,即x-2=0,
解得:x=2,y=1,
则原式=2.
点评 此题考查了分式的化简求值,以及二次根式有意义的条件,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是关于x,y的二元一次方程x-ay=3的一个解,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
5. 如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
 如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )
如图,正五边形的边长为2,连结对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.sin30°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
 学校新年联欢会上某班矩形有奖竞猜活动,猜对问题的同学即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖品分别为台灯、笔记本、签字笔.请问:
学校新年联欢会上某班矩形有奖竞猜活动,猜对问题的同学即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖品分别为台灯、笔记本、签字笔.请问: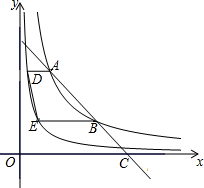 如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$.
如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$. 解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来.
解不等式$\frac{1+x}{3}<x-1$,并将解集在数轴上表示出来. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.
如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为2$\sqrt{2}$或4-2$\sqrt{2}$.