题目内容
10. 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2$\sqrt{2}$,BM=1,则MN的长为$\frac{5}{3}$.
分析 延长BC到G,使BG=DF连接AG,在AG截取AH=AN,连接MH、BH,证得RT△ABG≌RT△ADF,△AMN≌△AMH,△DFN≌△BGH,△AEF≌△AEG,最后利用等量代换求得答案即可.
解答 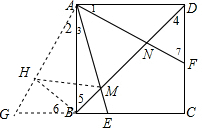 解:如图,延长BC到G,使BG=DF连接AG,在AG截取AH=AN,连接MH、BH.
解:如图,延长BC到G,使BG=DF连接AG,在AG截取AH=AN,连接MH、BH.
∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠4=∠5=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,
在RT△ABG和RT△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABG=∠ADF=90°}\\{BG=DF}\end{array}\right.$,
∴RT△ABG≌RT△ADF(SAS),
∴∠1=∠2,∠7=∠G,AF=AG,
∴∠GAE=∠2+∠3=∠1+∠3=∠BAD-∠EAF=90°-45°=45°=∠EAF,
在△AMN和△AMH中,
$\left\{\begin{array}{l}{AN=AH}\\{∠MAN=∠MAH=45°}\\{AM=AM}\end{array}\right.$,
∴△AMN≌△AMH(SAS),
∴MN=MH,
∵AF=AG,AN=AH,
∴FN=AF-AN=AG-AH=GH,
在△DFN和△BFH中,
$\left\{\begin{array}{l}{DF=BG}\\{∠7=∠G}\\{FN=GH}\end{array}\right.$,
∴△DFN≌△BGH(SAS),
∴∠6=∠4=45°,DN=BH,
∴∠MBH=∠ABH+∠5=∠ANG-∠6+∠5=90°-45°+45°=90°
∴BM2+DN2=BM2+BH2=MH2=MN2,
∵BD=$\sqrt{2}$AB=4,
∴12+(4-1-MN)2=MN2,
∴MN=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 此题考查正方形的性质,三角形全等的判定与性质,条件多而复杂,注意知识的综合运用与转化.

 单元期中期末卷系列答案
单元期中期末卷系列答案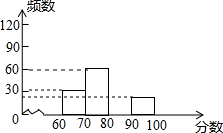 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:| 分段数 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 60 | n |
| 80≤x<90 | ||
| 90≤x<100 | 20 | 0.1 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
| A. | 5、7、3 | B. | 7、13、10 | C. | 5、7、2 | D. | 5、10、6 |
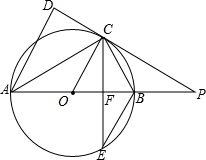 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,连接BE 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.