题目内容
3.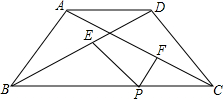 如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.
分析 根据平行线分线段成比例定理得出$\frac{PF}{DC}$=$\frac{PB}{BC}$,$\frac{PE}{AB}$=$\frac{CP}{BC}$,则$\frac{PB}{BC}$+$\frac{CP}{BC}$=1,进而得出x的值.
解答 解:不变化,
理由如下:
∵PF∥AB,PE∥CD,
∴$\frac{PF}{DC}$=$\frac{PB}{BC}$,$\frac{PE}{AB}$=$\frac{CP}{BC}$,则$\frac{PB}{BC}$+$\frac{CP}{BC}$=1,
∵AB=DC=3,
∴$\frac{PE}{3}$+$\frac{PF}{3}$=1,
∴$\frac{PE+PF}{3}$=1,
即PE+PF=3,则x=3.
点评 此题主要考查了平行线分线段成比例定理,根据已知得$\frac{PB}{BC}$+$\frac{CP}{BC}$=1是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.用代入法解方程组:$\left\{\begin{array}{l}2y-3x=1\\ x=y-1\end{array}\right.$,下面的变形正确的是( )
| A. | 2y-3y+3=1 | B. | 2y-3y-3=1 | C. | 2y-3y+1=1 | D. | 2y-3y-1=1 |
12.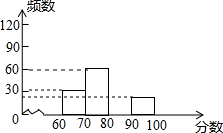 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
 “安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:
“安全教育,警钟长鸣”,为此,某中学组织全校1200名学生参加安全知识测试,为了解本次测试成绩的分布情况,从中随机抽取了部分学生的成绩,绘制出如下不完整的统计图表:| 分段数 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 60 | n |
| 80≤x<90 | ||
| 90≤x<100 | 20 | 0.1 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.3;
(2)补全频数分布直方图;
(3)测试成绩的中位数在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约为多少人?
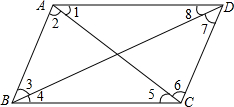 如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?
如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?
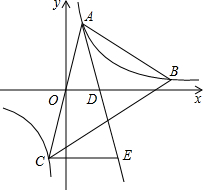 如图,在平面直角坐标系xOy中,点A($\frac{1}{2}$,2),B(3,n),在反比例函数y=$\frac{m}{x}$(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点D(1,0),过点C作CE∥x轴交直线l于点E.
如图,在平面直角坐标系xOy中,点A($\frac{1}{2}$,2),B(3,n),在反比例函数y=$\frac{m}{x}$(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点D(1,0),过点C作CE∥x轴交直线l于点E.