题目内容
12.如图1,在平面直角坐标系xOy中,抛物线M:$y=-\frac{1}{2}{x^2}+5$经过点C(2,3),直线y=kx+b与抛物线相交于A、B两点,∠ACB=90°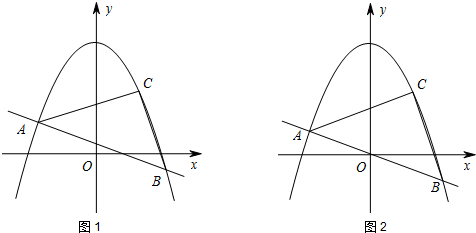
(1)探究与猜想
①探究:
取点B(6,-13)时,点A的坐标为($-\frac{5}{2}$,$\frac{15}{8}$),直接写出直线AB的解析式y=-$\frac{7}{4}$x-$\frac{5}{2}$;取点B(4,-3),直接写出AB的解析式为y=-$\frac{2}{3}$x-$\frac{1}{3}$
②猜想:
我们猜想直线AB必经过一个定点Q,其坐标为(-2,1).请取点B的横坐标为n,验证你的猜想;
友情提醒:此问如果没有解出,不影响第(2)问的解答
(2)如图2,点D在抛物线M上,若AB经过原点O,△ABD的面积等于△ABC的面积,试求出一个符合条件的点D的坐标,并直接写出其余的符合条件的D点的坐标.
分析 (1)①先求出点A坐标,再根据待定系数法即可解决问题.
②猜想直线AB必经过定点Q(-2,1),设A(m,-$\frac{1}{2}$m2+5),B(n,-$\frac{1}{2}$n2+5),过点C作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足分别为N、P,
由∠ACB=90°,△CAN∽△BCP,得$\frac{AN}{CN}$=$\frac{CP}{BP}$,得出m、n的关系,再联立方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+5}\\{y=kx+b}\end{array}\right.$,得$\frac{1}{2}$x2+kx+b-5=0,利用根与系数关系解决问题.
(2)①当CD∥AB时,△ABD的面积等于△ABC的面积,点D符合条件.
②求出直线CD与y轴的交点E,点E关于x轴的对称点F(0,-4),过点F平行AB的直线解析式为y=-$\frac{1}{2}$x-4,此时直线与抛物线的交点满足条件,利用方程组即可解决问题.
解答 解:(1)①设直线AB为y=kx+b,
∴$\left\{\begin{array}{l}{6k+b=-13}\\{-\frac{5}{2}k+b=\frac{15}{8}}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{7}{4}}\\{b=-\frac{5}{2}}\end{array}\right.$,
∴直线AB解析式为y=-$\frac{7}{4}$x-$\frac{5}{2}$,
∵B(4,-3),C(2,3),
∴直线边长为y=-3x+9,
∵AC⊥BC,
∴直线AC为y=$\frac{1}{3}$x+$\frac{7}{3}$,
由$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{7}{3}}\\{y=-\frac{1}{2}{x}^{2}+5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{8}{3}}\\{y=\frac{13}{9}}\end{array}\right.$,
∴点A坐标(-$\frac{8}{3}$,$\frac{13}{9}$),
∴直线AB解析式为y=-$\frac{2}{3}$x-$\frac{1}{3}$,
故答案分别为y=-$\frac{7}{4}$x-$\frac{5}{2}$,y=-$\frac{2}{3}$x-$\frac{1}{3}$,
②猜想直线AB必经过定点Q(-2,1),
验证如下:
设A(m,-$\frac{1}{2}$m2+5),B(n,-$\frac{1}{2}$n2+5),
过点C作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足分别为N、P,
∵∠ACB=90°,△CAN∽△BCP,
∴$\frac{AN}{CN}$=$\frac{CP}{BP}$,
∴$\frac{\frac{1}{2}{n}^{2}-2}{n-2}$=$\frac{2-m}{\frac{1}{2}{m}^{2}-2}$,
∴$\frac{\frac{1}{2}(n+2)(n-2)}{n-2}$=$\frac{2-m}{\frac{1}{2}(m+2)(m-2)}$,
∴(m+2)(n+2)=-4,
∴mn+2(m+n)+8=0,①
联立方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+5}\\{y=kx+b}\end{array}\right.$,
∴$\frac{1}{2}$x2+kx+b-5=0,
∴m+n=-2k,mn=2b-10,②
将②代入①,得化简,得
b=2k+1,
∵直线AB的解析式为y=kx+2k+1,即y=k(x+2)+1,
直线AB经过定点(-2,1)
(3)当直线AB经过原点,其解析式为y=-$\frac{1}{2}$x,
当CD∥AB时,△ABD的面积等于△ABC的面积,点D符合条件.
此时,直线CD的解析式为y=-$\frac{1}{2}$x+4.
则点D的横坐标是-$\frac{1}{2}$x2+5=-$\frac{1}{2}$x+4的根.
解得x1=2,x2=-1,其中x1=2是点C的横坐标.
当x=-1时,y=$\frac{9}{2}$,
∴D(-1,$\frac{9}{2}$),
∵直线CD交y轴于E(0,4),点E关于x轴的对称点F(0,-4),
过点F平行AB的直线解析式为y=-$\frac{1}{2}$x-4,此时直线与抛物线的交点满足条件,
由$\left\{\begin{array}{l}{y=-\frac{1}{2}{x}^{2}+5}\\{y=-\frac{1}{2}x-4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1+\sqrt{73}}{2}}\\{y=-\frac{17+\sqrt{73}}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{1-\sqrt{73}}{2}}\\{y=-\frac{17-\sqrt{73}}{4}}\end{array}\right.$,
∴D点坐标分别为($\frac{1+\sqrt{73}}{2}$,-$\frac{17+\sqrt{73}}{4}$)和($\frac{1-\sqrt{73}}{2}$,-$\frac{17-\sqrt{73}}{4}$).
∴其余符合条件的D点坐标分别为($\frac{1+\sqrt{73}}{2}$,-$\frac{17+\sqrt{73}}{4}$)和($\frac{1-\sqrt{73}}{2}$,-$\frac{17-\sqrt{73}}{4}$).
点评 本题考查了二次函数综合题、一次函数,平行线的性质等知识,解题的关键是灵活掌握待定系数法,学会利用方程组求两个函数的交点坐标,学会利用平行线的性质,寻找面积相等的三角形,属于中考压轴题.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | 11 cm | B. | 7.5 cm | C. | 11 cm或7.5 cm | D. | 以上都不对 |
 如图,点P是双曲线y=$\frac{6}{x}({x>0})$上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
如图,点P是双曲线y=$\frac{6}{x}({x>0})$上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 先增大后减小 | D. | 保持不变 |
| A. | x+4>y+4 | B. | -3x<-3y | C. | $\frac{x}{3}>\frac{y}{3}$ | D. | x2>y2 |
 如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )| A. | 80° | B. | 100° | C. | 90° | D. | 95° |
 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |
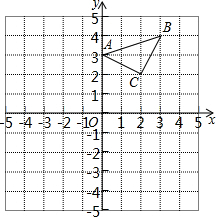 在平面直角坐标系中,△ABC的位置如图所示,将△ABC向左平移2个单位,再向下平移3个单位长度后得到△A′B′C′,((1)请在图中作出平移后的△A′B′C′
在平面直角坐标系中,△ABC的位置如图所示,将△ABC向左平移2个单位,再向下平移3个单位长度后得到△A′B′C′,((1)请在图中作出平移后的△A′B′C′