题目内容
2．已知方程组$\left\{\begin{array}{l}{3x+2y=2m+1}\\{2x+y=m-1}\end{array}\right.$，当m＞-2时，x+y＞0．分析 解此题首先要把字母m看做常数，然后解得x、y的值，结合题意，列得一元一次不等式，解不等式即可．
解答 解：$\left\{\begin{array}{l}{3x+2y=2m+1①}\\{2x+y=m-1②}\end{array}\right.$，
②×2-①得：x=-3③，
将③代入②得：y=m+5，
所以原方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=m+5}\end{array}\right.$，
∵x+y＞0，
∴-3+m+5＞0，
解得m＞-2，
∴当m＞-2时，x+y＞0．
故答案为＞-2．
点评 此题考查了二元一次方程组的解的定义，提高了学生的计算能力，解题的关键是把字母m看做常数，然后解二元一次方程组与一元一次不等式．
练习册系列答案
相关题目
13．如果a＞b，那么下列各式中正确的是（ ）
| A． | a-5＜b-5 | B． | $\frac{a}{3}$＜$\frac{b}{3}$ | C． | a+5＜b+5 | D． | -3a＜-3b |
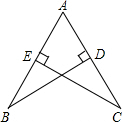如图，已知AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D，E，说明△ABD与△ACE全等的理由．
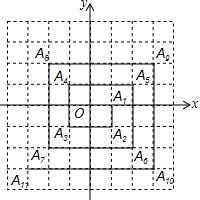如图，已知A1（1，0），A2（1，-1），A3（-1，-1），A4（-1，1），A5（2，1），…，则点A2017的坐标是（505，504）．
如图?ABCD中，AC平分∠DAB，AB=5cm，AC=8cm，则?ABCD的周长为20cm，面积为24cm2．