题目内容
11．若等腰三角形的周长为26cm，一边为11cm，则腰长为（ ）| A． | 11 cm | B． | 7.5 cm | C． | 11 cm或7.5 cm | D． | 以上都不对 |
分析 题中给出了周长和一边长，而没有指明这边是否为腰长，则应该分两种情况进行分析求解．
解答 解：①当11cm为腰长时，则腰长为11cm，底边=26-11-11=4cm，因为11+4＞11，所以能构成三角形；
②当11cm为底边时，则腰长=（26-11）÷2=7.5cm，因为7.5+7.5＞11，所以能构成三角形．
故选C．
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用，关键是利用三角形三边关系进行检验．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
1．
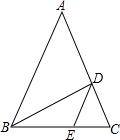如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，过点D作DE∥AB，交BC于点E，下列结论中错误的是（ ）
如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，过点D作DE∥AB，交BC于点E，下列结论中错误的是（ ）| A． | DE平分∠BDC | B． | △ABC∽△BDC∽△DEC | C． | $\frac{AD}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D． | $\frac{{S}_{△BCD}}{{S}_{△ABD}}$=$\frac{1}{2}$ |
2．下列图形中，不属于中心对称图形的是（ ）
| A． | 等边三角形 | B． | 菱形 | C． | 矩形 | D． | 平行四边形 |
如图，方格中的点A，B称为格点（格线的交点），以AB为一边画△ABC，其中是直角三角形的格点C的个数为（ ）
16．
如图，在平面直角坐标系中，点 B的坐标是（-2，0），点A是y轴正方向上的一点，且∠BAO=30°，现将△BAO顺时针旋转90°至△DCO，直线l是线段BC的垂直平分线，点P是l上一动点，则PA+PB的最小值为（ ）
如图，在平面直角坐标系中，点 B的坐标是（-2，0），点A是y轴正方向上的一点，且∠BAO=30°，现将△BAO顺时针旋转90°至△DCO，直线l是线段BC的垂直平分线，点P是l上一动点，则PA+PB的最小值为（ ）| A． | 2$\sqrt{6}$ | B． | 4 | C． | 2$\sqrt{3}$+1 | D． | 2$\sqrt{3}$+2 |
3．下列计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $\sqrt{8}=4$ | C． | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | D． | $\sqrt{（-3）^{2}}=-3$ |
