题目内容
13.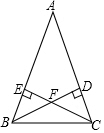 已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由.
已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由.
分析 首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BEC=∠CDB=90°,BC=CB,
在△BEC与△CDB中,
$\left\{\begin{array}{l}{∠ABC=∠ACB}\\{∠BEC=∠CDB=90°}\\{BC=BC}\end{array}\right.$,
∴△BEC≌△CDB (AAS),
∴∠DBC=∠ECB,
∴FB=FC,
∴△BFC是等腰三角形.
点评 本题考查了等腰三角形的性质和判定的应用,关键是根据AAS证明三角形全等和判定解答.

练习册系列答案
相关题目
3.已知△ABC与△DEF相似,且对应边的比为$\sqrt{2}$:1,则△ABC与△DEF的面积比为( )
| A. | 2:1 | B. | 1:2 | C. | $\sqrt{2}$:1 | D. | 1:$\sqrt{2}$ |
1.方程x2+17=8x的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
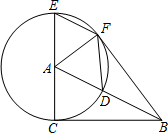 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.