题目内容
17.解下列方程:(1)x2-4x+1=0
(2)(x-2)(x-5)=-2.
分析 (1)把常数项1移项后,在左右两边同时加上4配方求解.
(2)原式整理为x2-7x+12=0,然后利用因式分解法求解.
解答 解:(1)x2-4x+1=0,
x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
∴x-2=$\sqrt{3}$或x-1=-$\sqrt{3}$
∴x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
(2)原式整理得:x2-7x+12=0,
(x-3)(x-4)=0,
∴x-3=0或x-4=0,
∴x1=3,x2=4.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.小张文具店每月一次性购进100件文具进行销售(能全部售出),有A,B两种文具可供选择,已知A型文具的进价是每件10元,B型文具的进价是每件15元,小张发现,所获总利润y(元)与A型文具的进货量x(件)之间存在着如下表所示的一次函数关系:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
| 购进A型文具x件 | … | 10 | 20 | 30 | 40 | 50 | … |
| 总利润y元 | … | 740 | 680 | 620 | 560 | 500 | … |
(2)在小张文具店中,B型文具的售价是23元;
(3)若在六月份,小张只有1300元,在进货量(100件)不变的前提下,六月份的最大利润是多少?
9.已知四边形ABCD,有以下四个条件:①AB∥CD;②BC∥AD;③AB=CD;④∠ABC=∠ADC.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
6.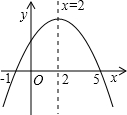 已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )
已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )
 已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )
已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )| A. | 关于x的方程ax2+bx+c=0的根是x1=-1,x2=5 | |
| B. | a-b+c>0 | |
| C. | b=-4a | |
| D. | ac<0 |
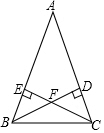 已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由.
已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由. 概念理解:
概念理解: 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10.
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10.