题目内容
4.化简:$\frac{x\sqrt{y}}{x\sqrt{y}-y\sqrt{x}}$-$\frac{y\sqrt{x}}{x\sqrt{y}+y\sqrt{x}}$,并任选一组你认为合适的x、y的值代入求值.分析 根据二次根式的性质即可求出答案.
解答 解:原式=$\frac{x\sqrt{y}(x\sqrt{y}+y\sqrt{x})}{{x}^{2}y-{y}^{2}x}$-$\frac{y\sqrt{x}(x\sqrt{y}-y\sqrt{x})}{{x}^{2}y-{y}^{2}x}$
=$\frac{{x}^{2}y+xy\sqrt{xy}-xy\sqrt{xy}+{xy}^{2}}{{x}^{2}y-{y}^{2}x}$
=$\frac{{x}^{2}y+x{y}^{2}}{{x}^{2}y-{y}^{2}x}$
=$\frac{xy(x+y)}{xy(x-y)}$
=$\frac{x+y}{x-y}$,
当x=1,y=2时,
原式=$\frac{1+2}{1-2}$
=-3
点评 本题考查二次根式的运算,解题的关键是熟练运用二次根式的运算法则,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某校八年级部分学生利用课外活动时间,积极参加篮球定点投篮的训练,训练结束后进行一次测试,记录如下表:
回答下列问题:
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 2 | 5 | 7 | 9 | 3 |
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
 如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.
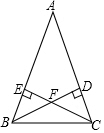 已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由.
已知:如图,在△ABC中,AB=AC,高BD和CE相交于点F,试说明△BFC是等腰三角形的理由.