题目内容
19.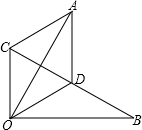 如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.
如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.(1)求∠COD度数;
(2)求证:四边形ODAC是菱形.
分析 (1)如图,根据题意证明△OBC为直角三角形,结合OC=$\frac{1}{2}BC$,求出∠B即可解决问题.
(2)首先证明AC∥OD,结合AC=OD,判断四边形ADOC为平行四边形,根据菱形的定义即可解决问题.
解答  解:(1)如图,由题意得:OC=OD=BD;
解:(1)如图,由题意得:OC=OD=BD;
∵点D是BC的中点,
∴CD=BD,OD=$\frac{1}{2}$BC,
∴△OBC为直角三角形,而OC=$\frac{1}{2}BC$,
∴∠B=30°,∠OCD=90°-30°=60°,;
∵OD=CD,
∴∠COD=∠OCD=60°.
(2)∵OD=BD,
∴∠DOB=∠B=30°,
由旋转变换的性质知:
∠COA=∠CAO=∠B=30°,
∴∠AOD=90°-2×30°=30°,
∴∠CAO=∠AOD=30°,
∴AC∥OD,而AC=OD,
∴四边形ADOC为平行四边形,而OC=OD,
∴四边形ODAC是菱形.
点评 该题主要考查了旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点及其应用问题;解题的关键是牢固掌握旋转变换的性质、直角三角形的判定、菱形的判定等几何知识点,并能灵活运用.

练习册系列答案
相关题目
 如图,已知△ABC.
如图,已知△ABC.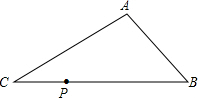 如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( ) 如图,∠1的同位角是∠B,∠B的内错角是∠3,∠4与∠B是同旁内角.
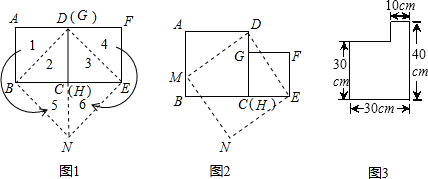
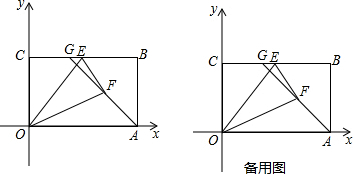
如图,∠1的同位角是∠B,∠B的内错角是∠3,∠4与∠B是同旁内角.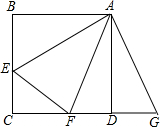 正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.