题目内容
解下列不等式,并在数轴上表示解集.
(1)
(4x-6)≤2(x-1)+x
(2)
-
<1.
(1)
| 1 |
| 2 |
(2)
| 3x+1 |
| 3 |
| 1-x |
| 2 |
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:计算题
分析:(1)先去掉括号,再进行移项,然后根据不等式的性质即可得出答案,从而画出数轴;
(2)先去掉分母,再去掉括号,然后合并同类项,再根据不等式的性质求解,最后画出数轴即可.
(2)先去掉分母,再去掉括号,然后合并同类项,再根据不等式的性质求解,最后画出数轴即可.
解答:解:(1)
(4x-6)≤2(x-1)+x,
2x-3≤2x-2+x,
2x-2x-x≤-2+3,
-x≤1,
x≥-1.

(2)
-
<1,
2(3x+1)-3(1-x)<6,
6x+2-3+3x<6,
9x<7,
x<
.

| 1 |
| 2 |
2x-3≤2x-2+x,
2x-2x-x≤-2+3,
-x≤1,
x≥-1.

(2)
| 3x+1 |
| 3 |
| 1-x |
| 2 |
2(3x+1)-3(1-x)<6,
6x+2-3+3x<6,
9x<7,
x<
| 7 |
| 9 |

点评:此题考查了解一元一次不等式,掌握解不等式的基本性质:不等式的两边同时加上或减去同一个数或整式不等号的方向不变;不等式的两边同时乘以或除以同一个正数不等号的方向不变;不等式的两边同时乘以或除以同一个负数不等号的方向改变是本题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图,正方形ABCD,M为AD上一点,N为DC延长线上一点,且MA=CN,连MB、NB、MN,E为MN中点,连EC.下列结论:
如图,正方形ABCD,M为AD上一点,N为DC延长线上一点,且MA=CN,连MB、NB、MN,E为MN中点,连EC.下列结论: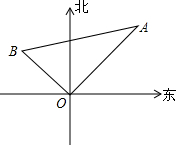 一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?
一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度? 如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积.
如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积.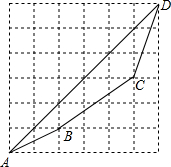 比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较
比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较 如图,△ABC中,D,E,F分别为BC,AC,AB的中点.
如图,△ABC中,D,E,F分别为BC,AC,AB的中点. 如图所示,已知∠1=110°,∠3=110°,∠4=70°
如图所示,已知∠1=110°,∠3=110°,∠4=70° 已知三角形ABC的两个顶点坐标为A(-4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为-1,求顶点C的坐标及三角形的面积.
已知三角形ABC的两个顶点坐标为A(-4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为-1,求顶点C的坐标及三角形的面积.