题目内容
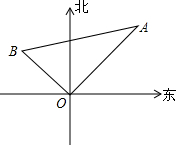 一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?
一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?考点:勾股定理的应用,方向角
专题:探究型
分析:先根据题意得出OA及OB的长,再根据勾股定理的逆定理判断出△OAB的形状,进而可得出结论.
解答: 解:由题意可知,OA=16+16×
解:由题意可知,OA=16+16×
=24(海里),OB=12+12×
=18(海里),AB=30海里,
∵242+182=302,即OA2+OB2=AB2,
∴△OAB是直角三角形,
∵∠AOD=40°,
∴∠BOD=90°-40°=50°,即另一艘轮船的航行的方向是北偏西50度.
 解:由题意可知,OA=16+16×
解:由题意可知,OA=16+16×| 1 |
| 2 |
| 1 |
| 2 |
∵242+182=302,即OA2+OB2=AB2,
∴△OAB是直角三角形,
∵∠AOD=40°,
∴∠BOD=90°-40°=50°,即另一艘轮船的航行的方向是北偏西50度.
点评:本题考查的是勾股定理的应用,根据题意判断出△AOB是直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、a
|
 某市有A,B,C,D四个超市,分别位于一条东西走向的大道附近,如图所示,请建立适当的坐标系,并写出四个超市相应的实际坐标.
某市有A,B,C,D四个超市,分别位于一条东西走向的大道附近,如图所示,请建立适当的坐标系,并写出四个超市相应的实际坐标. 如图所示,正方形ABCD中,E、F分别是AB和AD上的点,若CE⊥BF于点M,
如图所示,正方形ABCD中,E、F分别是AB和AD上的点,若CE⊥BF于点M,
 如图所示,AD是△ABC的高,AB=10,AD=8,BC=12,求证:△ABC是等腰三角形.
如图所示,AD是△ABC的高,AB=10,AD=8,BC=12,求证:△ABC是等腰三角形.