题目内容

14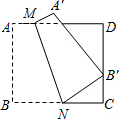．如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的点B′处，点A的对应点为点A′，且B′C=3，则B′N的长是（　　）
A．3B．4C．5D．4.5

分析 根据翻折变换的性质得到B′N=BN，根据勾股定理列出方程，解方程得到答案．

解答 解：由题意得，B′N=BN，CN=9-BN，
由勾股定理得，B′N2=B′C2+CN2，
即B′N2=32+（9-B′N）2，
解得，B′N=5，
故选：C．

点评 本题考查的是翻折变换的性质和正方形的性质，找出翻折变换中对应相等的线段和角是解题的关键，注意勾股定理和方程思想的准确运用．

练习册系列答案
相关题目
4．某批发商购进一批T恤，平均每天卖出200件，每件盈利30元；批发商为增加销量，决定降价销售，根据市场调查，单价每降低1元，每天可多卖出10件，但最低单价仍高于进价，设单价降低x元．
（1）用含x代数式表示：降价后销售T恤每件盈利（30-x）元，每天可售出（200+10x）件；
（2）降价后该批发商某一天销售T恤共获利6250元，求这一天单价降低了多少元．
5．某商场对2011年端午节这天销售A，B，C三种品牌粽子的情况进行了统计，并绘制出如图1和如图2所示的统计图，根据图中信息解答下列问题：
（1）哪一种品牌的粽子的销售量最大？说明理由；
（2）求出A品牌粽子在图2中所对应的圆心角的度数；
（3）补全图1，图2中的条形统计图和扇形统计图．
2．在等腰△ABC和等腰△DEF中，∠A与∠D是顶角，下列判断不正确的是（　　）
A．∠A=∠D时，两三角形相似B．∠A=∠E时，两三角形相似
C．∠B=∠E时，两三角形相似D．$\frac{AB}{BC}=\frac{DF}{EF}$时，两三角形相似
9．已知：⊙O1、⊙O2的半径分别为3和6，且圆心距O1O2=3，则这两圆的位置关系是（　　）
A．内切B．外切C．相交D．内含
19．某企业信息部进行市场凋研发现：
信息一：如果单独投资A种产品．则所获利润 yA（万元）与投资金额x（万元）之间存在正比例函数关系：yA=kx，并且当投资5万元时．可获利润2万元．
信息二：如果单独投资B种产品．则所获利润yB（万元）与投资金额x（万元）之间存在二次函数关系：yB=ax2+bx．并且当投资2万元时．可获利润2.4万元；当投资4万元时，可获利润3.2万元．
（1）请分别求出上述正比例函数表达式与二次函数表达式；
（2）若该企业同时投资A种产品7万元，B种产品3万元，这样能获得的利润是多少？
6．已知：a，b，c是非零有理数，且a+b+c=0，求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$的值．
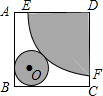3．要按图所示的方式，剪裁边长为a正方形铁片，以扇形EDF为侧面、⊙O为底面制作圆锥模型．设DE=R，⊙O的半径为r．
（1）写出R与r的关系；
（2）当a=5$\sqrt{2}$+2时，求r的值．
4．已知，若B（-2，0），A为象限内一点，且点A坐标是二元一次方程x+y=0的一组解，请你写出一个满足条件的点A坐标（-1，1）（写出一个即可），此时△ABO的面积为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网