题目内容
13.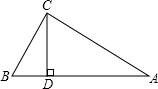 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.
如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.
分析 在Rt△ABC中,根据∠A的度数和AB的长,可求得BC的值;同理可在Rt△BCD中,根据∠BCD的度数和BC的长,求出BD的值.
解答 解:∵Rt△ABC中,∠ACB=90°,AB=5,∠A=30°,
∴BC=$\frac{1}{2}$AB=2.5;∠B=90°-∠A=60°.
∵Rt△BCD中,BC=2.5,∠BCD=90°-∠B=30°,
∴BD=$\frac{1}{2}$BC=1.25.
点评 此题主要考查的是直角三角形的性质:在直角三角形中,30°角所对直角边等于斜边的一半.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
18.在等腰三角形中,顶角是36°,则底角是( )
| A. | 72° | B. | 36° | C. | 70° | D. | 80° |
3.下列说法中错误的是( )
| A. | 正数都大于0 | |
| B. | 负数都小于0 | |
| C. | 正数大于一切负数 | |
| D. | 数轴上表示的两个数,左边的数总比右边的数大 |
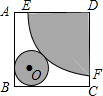 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.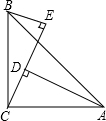 已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.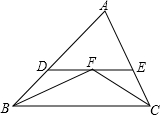 如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证:
如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证: