题目内容
7.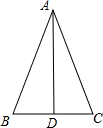 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
分析 首先根据角平分线定义可得到∠BAD=∠CAD,再利用SAS定理可证明△ABD≌△ACD.
解答 证明:∵AD平分∠BAC(已知).
∴∠BAD=∠CAD(角平分线定义),
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC(已知)}\\{∠BAD=∠CAD(已证)}\\{AD=AD(公共边)}\end{array}\right.$,
∴△ABD≌△ACD (SAS).
点评 此题主要考查了全等三角形的判定,判定两个一般三角形全等的方法有四种:AAS,SAS,SSS,ASA.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.抛物线y=x2-2x-1与x轴交点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
2.已知线段AB=3cm,反向延长线段AB到C,使BC=$\frac{5}{3}$AC,D是BC的中点,则线段AD的长为( )
| A. | $\frac{5}{2}$cm | B. | $\frac{5}{4}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{1}{4}$cm |
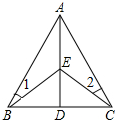 如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由.
如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由. 如图,网格中每个小正方形的边长都是1,且A,B,C,D都在格点上.
如图,网格中每个小正方形的边长都是1,且A,B,C,D都在格点上.