题目内容
17.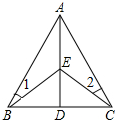 如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由.
如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由.
分析 由等腰三角形的性质和已知条件得出∠ABC=∠ACB,由等角对等边得出AB=AC,由SAS证明△ABE≌△ACE,得出对应角相等∠BAD=∠CAD,再由等腰三角形的三线合一性质即可得出结论.
解答 解:AD⊥BC,理由如下:
∵EB=EC,
∴∠EBC=∠ECB,
∵∠1=∠2,
∴∠EBC+∠1=∠ECB+∠2,
即∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACE中,
$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠ABC=∠ACB}&{\;}\\{EB=EC}&{\;}\end{array}\right.$,
∴△ABE≌△ACE(SAS),
∴∠BAD=∠CAD,
即AD平分∠BAC,
又∵AB=AC,
∴AD⊥BC.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
10.已知m+n-3(m-2n)=P,-5m-4n+(6m-4n)=Q,则m+n的结果( )
| A. | P+Q | B. | -P-Q | C. | P | D. | -Q |
 如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.
如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB. 正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度. 萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: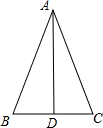 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.