题目内容
18.抛物线y=x2-2x-1与x轴交点的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
分析 先计算判别式的值,然后根据△=b2-4ac>0时,抛物线与x轴有2个交点进行判断.
解答 解:∵△=(-2)2-4×1×(-2)=12>0,
∴抛物线y=x2-2x-1与x轴有两交点.
故选C.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知m+n-3(m-2n)=P,-5m-4n+(6m-4n)=Q,则m+n的结果( )
| A. | P+Q | B. | -P-Q | C. | P | D. | -Q |
3.已知△ABC≌△DEF,∠A=∠D=90°,∠B=43°,则∠E的度数是( )
| A. | 43° | B. | 47° | C. | 47°或43° | D. | 43°或57° |
10.已知两边及其中一边的对角作三角形,下列结论正确的是( )
| A. | 有唯一一个三角形 | B. | 不能作出三角形 | ||
| C. | 有两个三角形 | D. | 以上三种情况都有可能 |
 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度. 萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: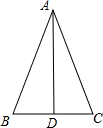 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.