题目内容
19.在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;③∠A:∠B:∠C=2:3:4; ④∠A=90°-∠C,能确定△ABC是直角三角形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由已知条件和三角形内角和定理得出能确定△ABC是直角三角形的有①②④,即可得出结论.
解答 解:①∵∠A=60°,∠C=30°,
∴∠C=180°-60°-30°=90°,
∴△ABC是直角三角形,①能确定;
②∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,②能确定;
③∵∠A:∠B:∠C=2:3:4,∠A+∠B+∠C=180°,
∴∠C=80°,
∴△ABC是锐角三角形,③不能确定;
④∵∠A=90°-∠C,∠A+∠B+∠C=180°,
∴∠B=90°,
∴△ABC是直角三角形,④能确定;
能确定△ABC是直角三角形的有3个.
故选:C.
点评 本题考查了三角形内角和定理、直角三角形的判定方法;熟练掌握三角形内角和定理,求出△ABC中的最大角是解决问题的关键.

练习册系列答案
相关题目
10.已知两边及其中一边的对角作三角形,下列结论正确的是( )
| A. | 有唯一一个三角形 | B. | 不能作出三角形 | ||
| C. | 有两个三角形 | D. | 以上三种情况都有可能 |
4.若有理数x,y满足|x|=7,y2=16且|x-y|=y-x,则x+y的值( )
| A. | -11或-3 | B. | -11或3 | C. | 3或11 | D. | -3 |
 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.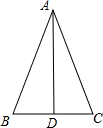 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.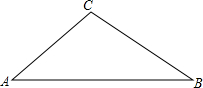 如图,在△ABC中,∠A=45°,tanB=$\frac{3}{4}$,BC=10,则AB的长为14.
如图,在△ABC中,∠A=45°,tanB=$\frac{3}{4}$,BC=10,则AB的长为14. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=$\frac{3}{5}$,BC=4,求AC的长.
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=$\frac{3}{5}$,BC=4,求AC的长.