题目内容
17.将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(4,0),点B(0,3),点O(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′.(1)如图①,当点A′与顶点B重合时,求点M的坐标;
(2)如图②,当动点M运动到边AO的中点时,求点O与点A′的距离.
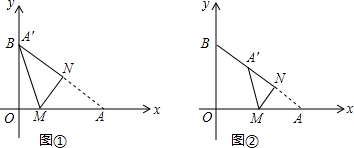
分析 (1)由勾股定理得出AB,由折叠的性质得出AN=BN=$\frac{1}{2}$AB=2.5,证明△AMN∽△ABO,得出对应边相等$\frac{AM}{AB}=\frac{AN}{OA}$,求出AM,得出OM即可;
(2)连接OA′,由(1)得:△AMN∽△ABO,得出$\frac{AM}{AB}=\frac{AN}{OA}$,求出AN=$\frac{8}{5}$,由折叠的性质得:A′N=AN=$\frac{8}{5}$,A′A=$\frac{16}{5}$,MN是△OAA′的中位线,由三角形中位线定理得出MN∥OA′,∠AA′O=∠ANM=90°,由勾股定理求出OA′即可.
解答 解:(1)∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
由折叠的性质得:AN=BN=$\frac{1}{2}$AB=2.5,∠ANM=90°=∠AOB,
∵∠NAM=∠OAB,
∴△AMN∽△ABO,
∴$\frac{AM}{AB}=\frac{AN}{OA}$,
即$\frac{AM}{5}=\frac{2.5}{4}$,
解得:AM=$\frac{25}{8}$,
∴OM=OA-AM=4-$\frac{25}{8}$=$\frac{7}{8}$,
∴M($\frac{7}{8}$,0);
(2)连接OA′,如图所示:
∵M是AO的中点,
∴AM=OM=2,
由(1)得:△AMN∽△ABO,
∴$\frac{AM}{AB}=\frac{AN}{OA}$,即$\frac{2}{5}=\frac{AN}{4}$,
解得:AN=$\frac{8}{5}$,
由折叠的性质得:A′N=AN=$\frac{8}{5}$,
∴A′A=$\frac{16}{5}$,MN是△OAA′的中位线,
∴MN∥OA′,∠AA′O=∠ANM=90°,
∴OA′=$\sqrt{O{A}^{2}-A′{A}^{2}}$=$\sqrt{{4}^{2}-(\frac{16}{5})^{2}}$=$\frac{12}{5}$.
点评 本题考查了翻折变换的性质、勾股定理、三角形中位线定理、相似三角形的判定与性质;本题有一定难度,特别是(2)中,运用勾股定理和三角形中位线定理得出结果是解决问题的关键.

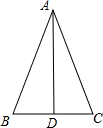 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.请补充完整证明△ABD≌△ACD的过程和理由. 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=$\frac{3}{5}$,BC=4,求AC的长.
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=$\frac{3}{5}$,BC=4,求AC的长.