题目内容
11. 如图,矩形ABCD中,AB=4,BC=8,把△BCD沿对角线BD翻折得到△BC′D,连接AC′,则线段AC′的长度为( )
如图,矩形ABCD中,AB=4,BC=8,把△BCD沿对角线BD翻折得到△BC′D,连接AC′,则线段AC′的长度为( )| A. | $\frac{12}{5}$ | B. | 4 | C. | $\frac{12\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
分析 设AD与BC′交于点F.根据矩形的性质得出AD=BC=8,AD∥BC,∠BAD=90°.设FD=x,则AF=8-x,根据折叠的性质得到∠CBD=∠C′BD.由AD∥BC,得出∠ADB=∠CBD,那么∠C′BD=∠ADB,BF=FD=x.在直角△AFB中根据勾股定理得出x2=(8-x)2+16,解方程求出x=5,则BF=FD=5,AF=8-x=3.然后根据△AFC′∽△DFB,利用相似三角形对应边成比例求出AC′=$\frac{12\sqrt{5}}{5}$.
解答 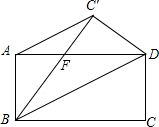 解:如图,设AD与BC′交于点F.
解:如图,设AD与BC′交于点F.
∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,∠BAD=90°.
设FD=x,则AF=8-x,
∵把△BCD沿对角线BD翻折得到△BC′D,
∴∠CBD=∠C′BD.
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠C′BD=∠ADB,
∴BF=FD=x.
在直角△AFB中,∵∠BAF=90°,AB=4,AF=8-x,BF=x,
∴x2=(8-x)2+16,
解之得,x=5,
则BF=FD=5,AF=8-x=3.
∵△AFC′∽△DFB,
∴$\frac{AC′}{BD}$=$\frac{AF}{DF}$,即$\frac{AC′}{\sqrt{{4}^{2}+{8}^{2}}}$=$\frac{3}{5}$,
解得AC′=$\frac{12\sqrt{5}}{5}$.
故选C.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.同时考查了矩形的性质,平行线的性质,相似三角形的判定与性质以及勾股定理.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
2.我们学习了整式的乘法后,可进行如下计算:(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3;
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
上表称为“杨辉三角”,揭示了二项式乘方展开式的规律.
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
| (a+b)1=a+b | 1 | 1 | ||||||||
| (a+b)2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| (a+b)3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| … | … |
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
6. 如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
 如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 25cm |
20.抛物线y=-$\frac{1}{2}$(x+2)2-1顶点坐标是( )
| A. | (2,-1) | B. | (2,1) | C. | (-2,-1) | D. | (-2,1) |
 如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,求S四边形DBCE的值.
如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,求S四边形DBCE的值.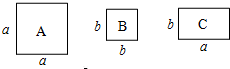 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.