题目内容
14.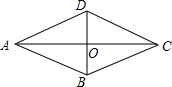 一个菱形的一条对角线长60cm.周长是200cm.求:
一个菱形的一条对角线长60cm.周长是200cm.求:(1)另一条对角线的长.
(2)这个菱形的面积.
分析 (1)根据菱形四条边都相等求出边长,再根据菱形的对角线互相垂直平分,利用勾股定理列式求出另一对角线的一半,从而得到另一对角线的长度;
(2)根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解答 解:∵菱形的周长是200cm,
∴菱形的边长为200÷4=50cm,
∵一条对角线长60cm,
∴该对角线的一半=60÷2=30cm,
∴另一对角线的一半=$\sqrt{5{0}^{2}-3{0}^{2}}$=40cm,
∴另一对角线长是40×2=80cm;
(2)由(1)可知这个菱形的面积=$\frac{1}{2}$×60×80=2400cm2.
点评 本题主要考查了菱形四条边都相等的性质,对角线互相垂直的性质,勾股定理的应用,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列图形:

其中是轴对称图形的共有( )

其中是轴对称图形的共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.我们学习了整式的乘法后,可进行如下计算:(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3;
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
上表称为“杨辉三角”,揭示了二项式乘方展开式的规律.
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
| (a+b)1=a+b | 1 | 1 | ||||||||
| (a+b)2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| (a+b)3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| … | … |
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
6. 如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
 如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 25cm |
 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.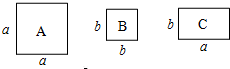 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.