题目内容
4.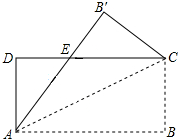 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
分析 由四边形ABCD为矩形及折叠的特性,得到B′C=BC=AD,∠B′=∠B=∠D=90°,∠B′EC=∠DEA,得到△AED≌△CEB′,根据全等三角形的性质即可得到结论.
解答 解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA,
在△AED和△CEB′中,$\left\{\begin{array}{l}{∠B′EC=∠DEA}\\{∠B′=∠D}\\{B′C=AD}\end{array}\right.$,
∴△AED≌△CEB′(AAS),
∴DE=B′E,
∴△EB′C的周长=CE+B′E+B′C=CE+DE+AD=11,
故答案为:11.
点评 本题主要考查了图形的折叠问题,全等三角形的判定和性质,及矩形的性质.熟记翻折前后两个图形能够重合找出相等的角是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.函数y=$\sqrt{x-1}$+2中,自变量x的取值范围是( )
| A. | x≥1 | B. | x>1 | C. | x<1 | D. | x≤1 |
12.下列整数中,与$\sqrt{5}$最接近的是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
9.对于二次函数y=x2-2mx-3,下列结论错误的是( )
| A. | 它的图象与x轴有两个交点 | B. | 方程x2-2mx=3的两根之积为-3 | ||
| C. | 它的图象的对称轴在y轴的右侧 | D. | x<m时,y随x的增大而减小 |
14.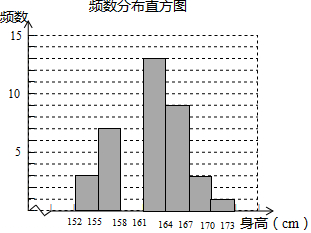 某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
根据以上统计图表完成下列问题:
(1)统计表中m=14,n=0.26,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在:161≤x<164范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
 某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.
某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表.| 身高分组 | 频数 | 频率 |
| 152≤x<155 | 3 | 0.06 |
| 155≤x<158 | 7 | 0.14 |
| 158≤x<161 | m | 0.28 |
| 161≤x<164 | 13 | n |
| 164≤x<167 | 9 | 0.18 |
| 167≤x<170 | 3 | 0.06 |
| 170≤x<173 | 1 | 0.02 |
(1)统计表中m=14,n=0.26,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在:161≤x<164范围内;
(3)在身高≥167cm的4人中,甲、乙两班各有2人,现从4人中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
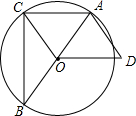 如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.
如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.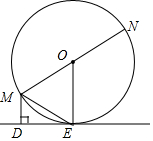 已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.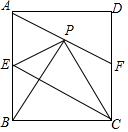 如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).
如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).