题目内容
12.计算(1)(-$\frac{1}{4}$)-1-1-2×(-22)-($\frac{1}{2}$)-2
(2)(-a2)3-(-a3)2+2a5•(-a)
(3)($\frac{1}{2}$x-y)2-$\frac{1}{4}$(x+2y)(x-2y)
(4)(3-2x+y)(3+2x-y)
分析 (1)根据负整数指数幂的意义计算;
(2)先进行乘方运算,然后合并即可;
(3)先利用完全平方公式和平方差公式展开,然后合并即可;
(4)先变形得到原式=[3+(2x-y)][3-(2x-y)],然后利用平方差公式和完全平方公式计算.
解答 解:(1)原式=-4-1×(-4)-4
=-4+4-4
=-4;
(2)原式=-a6-a6-2a6
=-4a6;
(3)原式=$\frac{1}{4}$x2-xy+y2-$\frac{1}{4}$(x2-4y2)
=$\frac{1}{4}$x2-xy+y2-$\frac{1}{4}$x2+y2
=2y2-xy;
(4)原式=[3+(2x-y)][3-(2x-y)]
=32-(2x-y)2
=9-(4x2-4xy+y2)
=9-4x2+4xy-y2.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
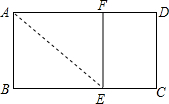 如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=$\frac{\sqrt{5}+1}{2}$.
如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=$\frac{\sqrt{5}+1}{2}$.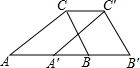 如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.
如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.

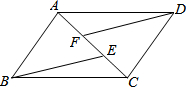 如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.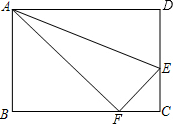 小红用一张长方形纸片ABCD进行折纸,已知该纸片宽8,长BC为10,当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),想一想,此时FC有多长?
小红用一张长方形纸片ABCD进行折纸,已知该纸片宽8,长BC为10,当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),想一想,此时FC有多长?