题目内容
20.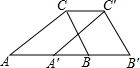 如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.
如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.
分析 根据线段中点的定义求出AA′,再根据平移的性质可得A′B′=AB,然后根据AB′=AA′+A′B′计算即可得解.
解答 解:∵A′C′恰好经过BC边的中点D,
∴AA′=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∵△ABC沿射线AB方向平移得到△A′B′C′,
∴A′B′=AB,
∴AB′=AA′+A′B′=2+4=6.
故答案为:6.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
10.计算(-2x2)2•(-3x)3的结果是( )
| A. | 40x7 | B. | -40x7 | C. | -108x7 | D. | 400x7 |
8.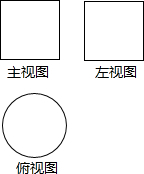 如图所示是一个几何体的三视图,这个几何体的名称是( )
如图所示是一个几何体的三视图,这个几何体的名称是( )
 如图所示是一个几何体的三视图,这个几何体的名称是( )
如图所示是一个几何体的三视图,这个几何体的名称是( )| A. | 圆柱 | B. | 三棱锥 | C. | 球 | D. | 圆锥 |
15.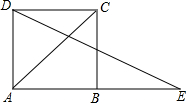 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )| A. | 45° | B. | 30° | C. | 22.5° | D. | 15° |
 如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.
如图,在等腰△ABC中,AB=AC=8,BC=6,AB的垂直平分线MN交AC于点D,则△DBC的周长为14.