题目内容
4.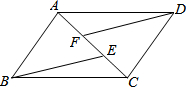 如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
分析 利用平行四边形的性质得出∠BAC=∠DCF,进而利用全等三角形的判定与性质得出答案.
解答 证明:∵AF=CE,
∴AE=FC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠BAC=∠DCF,
在△ABE和△CDF中
∵$\left\{\begin{array}{l}{AB=DC}\\{∠BAE=∠DCF}\\{AE=FC}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠ABE=∠CDF.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质,正确得出△ABE≌△CDF是解题关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
15.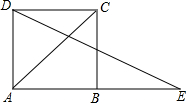 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
 如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )
如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=( )| A. | 45° | B. | 30° | C. | 22.5° | D. | 15° |
16.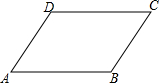 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
 如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )
如图,在平行四边形ABCD中,如果∠A=50°,则∠C=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
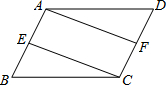 如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.
如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.