题目内容
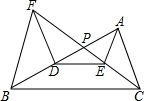如图，在△ABC中，点D是AB上一点，E是△ABC内一点，DE∥BC，过点D作AC的平行线交CE的延长线于点F，CF与AB交于P，求证：BF∥AE．考点：相似三角形的判定与性质
专题：证明题
分析：易证△PDE∽△PBC和△PDF∽△PAC，可得
=
和
=
，即可求得
=
，即可证明△PAE∽△PBF，可得∠PAE=∠PBF，即可解题．
| PD |
| PB |
| PE |
| PC |
| PD |
| PA |
| PF |
| PC |
| PB |
| PA |
| PF |
| PE |
解答：证明：∵DE∥BC，
∴△PDE∽△PBC，
∴
=
，即PD•PC=PB•PE，①
∵DF∥AC，
∴△PDF∽△PAC，
∴
=
，即PD•PC=PA•PF，②
由①②得：PE•PB=PA•PF，
∴
=
，
∵∠APE=∠BPF，
∴△PAE∽△PBF，
∴∠PAE=∠PBF，
∴BF∥AE．
∴△PDE∽△PBC，
∴
| PD |
| PB |
| PE |
| PC |
∵DF∥AC，
∴△PDF∽△PAC，
∴
| PD |
| PA |
| PF |
| PC |
由①②得：PE•PB=PA•PF，
∴
| PB |
| PA |
| PF |
| PE |
∵∠APE=∠BPF，
∴△PAE∽△PBF，
∴∠PAE=∠PBF，
∴BF∥AE．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△PAE∽△PBF是解题的关键．
练习册系列答案
相关题目
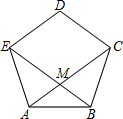正五边形ABCDE的对角线AC、BE相交于点M．
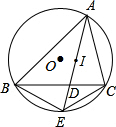如图，△ABC内接于⊙O，I是△ABC的内心，AI交BC于点D，交⊙O于点E，试说明BE、CE、IE的大小关系．
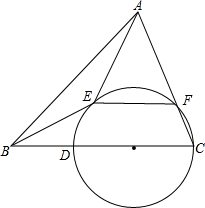在△ABC中，∠B=45°，D为BC边上一点，DC=2BD，以DC为直径作⊙O交AD于点E，交AC于点F，连BE，若∠ADC=60°
如图，点O为直线AB上一点，∠AOC=50°．