题目内容
 如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )
如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )| A、1:2 | B、2:3 |
| C、1:4 | D、2:5 |
考点:相似三角形的判定与性质,三角形中位线定理,平行四边形的性质
专题:
分析:先根据平行四边形的性质得出OB=OD,由EF=FD,根据三角形的中位线定理可得BE=2OF,BE∥OF,再由AE=EF,可得AG=GO,再由中位线定理可得GE=
OF,进而求出GE与BE的比值.
| 1 |
| 2 |
解答:解:∵四边形ABCD是平行四边形,
∴OB=OD,
∵EF=FD,
∴OF=
BE,OF∥BE,
即BE=2OF
又∵AE=EF
∴AG=GO
∴GE=
OF
∴BE:GE=2OF:
OF=1:4.
故选C.
∴OB=OD,
∵EF=FD,
∴OF=
| 1 |
| 2 |
即BE=2OF
又∵AE=EF
∴AG=GO
∴GE=
| 1 |
| 2 |
∴BE:GE=2OF:
| 1 |
| 2 |
故选C.
点评:本题主要考查了平行四边形的性质和三角形的中位线定理,解题的关键是在两个三角形中运用中位线定理,寻找两条线段之间的关系,进而求出问题的答案.

练习册系列答案
相关题目
2014年某公司购进耗材约2015000000元,2015000000元用科学记数法表示为( )
| A、2.015×109元 |
| B、2.015×107元 |
| C、2.015×1011元 |
| D、2.015×106元 |
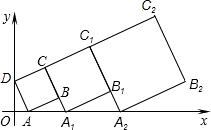 在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为
在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为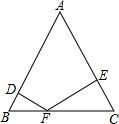 如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.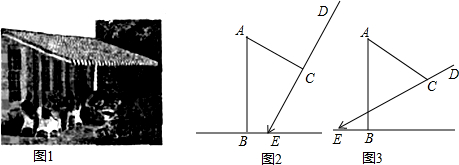
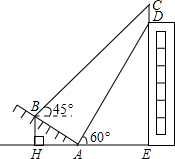 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
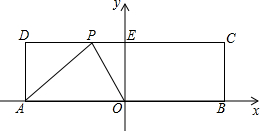 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标. 如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么?
如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么?