题目内容

如图，点E在DF上，点B在AC上，BD∥CE，∠C=∠D，∠A与∠F相等吗？为什么？
考点：平行线的判定与性质
专题：
分析：根据平行线的性质得出∠C=∠DBA，求出∠D=∠DBA，根据平行线的判定得出DF∥AC，即可得出答案．
解答：解：∠A=∠F，
理由是：∵BD∥CE，
∴∠C=∠DBA，
∵∠C=∠D，
∴∠D=∠DBA，
∴DF∥AC，
∴∠A=∠F．
点评：本题考查了平行线的性质和判定的应用，能正确运用平行线的性质和判定定理进行推理是解此题的关键，难度适中．
练习册系列答案
相关题目
如图，在?ABCD中，AC与BD相交于点O，AE=EF=FD，BE交AC于G，则GE：BE=（　　）
A、1：2B、2：3
C、1：4D、2：5
对于抛物线y=-（x-1）2+2，下列说法中错误的是（　　）
A、对称轴是直线x=1
B、顶点坐标是（1，2）
C、当x＞1时，y随x的增大而减小
D、当x=1时，函数y的最小值为2
在一个不透明的盒子中，放入2个白球和1个红球，这些球除颜色外都相同．
（1）搅匀后从中任意摸出1个球，记录下颜色后放回袋中，再次搅匀后从中任意摸出1个球，请通过列表或画树状图求2次摸出的球都是白球的概率；
（2）搅匀后从中任意一次摸出2个球，则摸出的2个球都是白球的概率为
 
；
（3）现有一个可以自由转动的转盘，转盘被等分成60个相等的扇形，这些扇形除颜色外完全相同，其中40个扇形涂上白色，20个扇形涂上红色，转动转盘2次，指针2次都指向白色区域的概率为
 
．
芳芳用水管以均匀的速度向一个容器中注水，在注水过程中，水面的高度h与注水时间t之间的函数图象如图所示，最后芳芳将容器注满水，则这个容器的形状大致为（　　）
A、
B、
C、
D、
如图，已知A（a，b），AB⊥y轴于B，且满足|a-2|+（b-2）2=0，
（1）求A点坐标；
（2）如图1，分别以AB，AO为边作等边三角形△ABC和△AOD，试判定线段AC和DC的数量关系和位置关系，并说明理由；
（3）如图2，过A作AE⊥x轴于E，点F、G分别为线段OE、AE上的两个动点，满足∠FBG=45°，试探究
OF+AG
FG
的值是否发生变化？如果不变，求其值；如果变化，请说明理由．
靠墙摆放梯子时，若梯子底端离墙的距离为梯子长度的
1
3
，则梯子比较稳定．
（1）当梯子稳定摆放的情况下，3米的梯子能达到多高的墙？（结果保留根号）
（2）要达到4米高的墙头，梯子至少要多长？（结果保留根号）
北京两会期间，记者随机抽取参会的部分代表，对他们某天发表提议的次数进行统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发表提议的人数的比为5：2，请结合图中相关数据回答下列问题：
发表提议次数“n”
A0≤n＜3
B3≤n＜6
C6≤n＜9
D9≤n＜12
E12≤n＜15
F15≤n＜18
（1）求出样本容量，并补全直方图；
（2）会议期间组织1700名代表调研，请估计在这一天里发表提议次数不少于12次的人数；
（3）已知A组发表提议的代表中恰有1为女士，E组发表提议的代表中只有2位男士，现从A组与E组中分别抽一位代表写报告，请用列表法或画树状图的方法，求所抽的两位代表恰好是一男一女的概率．
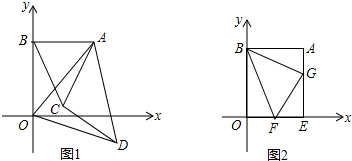
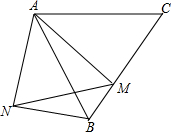如图，M是等边△ABC的边BC上一点，以AM为一边向外作等边△AMN，连接NB，请找出图中的一组全等三角形，并进行证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网