题目内容
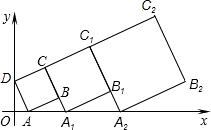 在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为
在平面直角坐标系xOy中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为考点:相似三角形的判定与性质,正方形的性质
专题:规律型
分析:根据相似三角形的判定原理,得出△AA1B∽△A1A2B1,继而得知∠BAA1=∠B1A1A2;利用勾股定理计算出正方形的边长;最后利用正方形的面积公式计算第一个正方形的面积,从中找出规律,进而可求出第n个正方形的面积.
解答:解:设正方形的面积分别为S1,S2…,Sn,
根据题意,得:AD∥BC∥C1A2∥C2B2,
∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=∠A2B2x=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD=
,tan∠ADO=
=
,
∵tan∠BAA1=
=tan∠ADO,
∴BA1=
AB=
,
∴CA1=
+
,
同理,得:C1A2=(
+
)×(1+
),
由正方形的面积公式,得:S1=(
)2=5,
S2=(
)2×(1+
)2,
S3=(
)2×(1+
)4=5×(
)4,
由此,可得Sn=(
)2×(1+
)2(n-1)=5×(
)2n-2.
故答案为:5;5×(
)2n-2.
根据题意,得:AD∥BC∥C1A2∥C2B2,

∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=∠A2B2x=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD=
| 5 |
| OA |
| OD |
| 1 |
| 2 |
∵tan∠BAA1=
| BA1 |
| AB |
∴BA1=
| 1 |
| 2 |
| ||
| 2 |
∴CA1=
| 5 |
| ||
| 2 |
同理,得:C1A2=(
| 5 |
| ||
| 2 |
| 1 |
| 2 |
由正方形的面积公式,得:S1=(
| 5 |
S2=(
| 5 |
| 1 |
| 2 |
S3=(
| 5 |
| 1 |
| 2 |
| 3 |
| 2 |
由此,可得Sn=(
| 5 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:5;5×(
| 3 |
| 2 |
点评:本题考查了正方形的性质,相似三角形的性质和判定,勾股定理的应用,解此题的关键是根据计算的结果得出规律,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若双曲线y=
与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
| k |
| x |
| A、-1 | B、1 | C、-2 | D、2 |
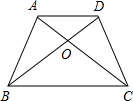
 如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )
如图,在?ABCD中,AC与BD相交于点O,AE=EF=FD,BE交AC于G,则GE:BE=( )| A、1:2 | B、2:3 |
| C、1:4 | D、2:5 |
对于抛物线y=-(x-1)2+2,下列说法中错误的是( )
| A、对称轴是直线x=1 |
| B、顶点坐标是(1,2) |
| C、当x>1时,y随x的增大而减小 |
| D、当x=1时,函数y的最小值为2 |
 如图,在等边三角形ABC中,∠ADE=60°.
如图,在等边三角形ABC中,∠ADE=60°.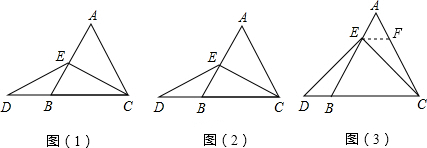
 如图,在梯形ABCD中,AD∥BC,AD=1,BC=2,若△AOD、△AOB、△BOC的面积分别为S1、S2、S3,则S1:S2:S3=
如图,在梯形ABCD中,AD∥BC,AD=1,BC=2,若△AOD、△AOB、△BOC的面积分别为S1、S2、S3,则S1:S2:S3=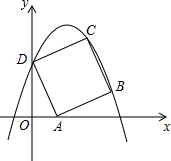 如图,在平面直角坐标系xOy中,边长为
如图,在平面直角坐标系xOy中,边长为