题目内容
7.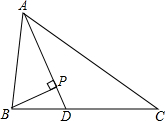 如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.
如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.
分析 先延长BP,交AC于E,根据已知条件、结合ASA易证△ABP≌△AEP,从而有BP=PE,AE=AB,∠AEB=∠ABE,易求BE=4,AE=5,那么CE=4,于是可知△BCE是等腰三角形,那么∠EBC=∠C,结合三角形外角性质可证∠ABE=2∠C.
解答 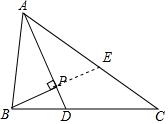 证明:延长BP,交AC于E,
证明:延长BP,交AC于E,
∵AD平分∠BAC,BP⊥AD,
∴∠BAP=∠EAP,∠APB=∠APE,
在△ABP与△AEP中,$\left\{\begin{array}{l}{∠BAP=∠EAP}\\{AP=AP}\\{∠APB=∠APE}\end{array}\right.$,
∴△ABP≌△AEP,
∴BP=PE,AE=AB,∠AEB=∠ABE,
∴BE=BP+PE=4,AE=AB=5,
∴CE=AC-AE=9-5=4,
∴CE=BE,
∴△BCE是等腰三角形,
∴∠EBC=∠C,
又∵∠ABP=∠AEB=∠C+∠EBC,
∴∠ABP=2∠C.
点评 本题考查了全等三角形的判定和性质、等腰三角形的判定和性质、三角形外角的性质.关键是作辅助线,求证△BCE是等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.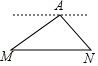 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | 400米 | D. | 200($\sqrt{3}+1$)米 |
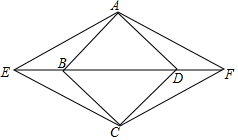 已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF.
已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF.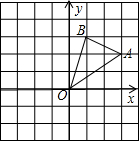 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3)