题目内容
5.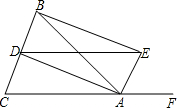 如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.
如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.
分析 求出∠AEB=90°,∠DAE=90°,根据等腰三角形性质求出∠BDA=90°,证出四边形AEBD是矩形即可.
解答 解:四边形AEBD是矩形;理由如下:
∵AD、AE分别是∠BAC和∠BAC和外角的平分线,
∴∠DAB=$\frac{1}{2}$∠CAB,∠BAE=$\frac{1}{2}$∠BAF,
∴∠DAE=∠DAB+∠BAE=$\frac{1}{2}$(∠CAB+∠ABF)=$\frac{1}{2}$×180°=90°,
∵AE⊥BE,
∴∠AEB=90°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
点评 本题考查了矩形的判定、等腰三角形性质、垂直定义、角平分线定义;熟练掌握矩形的判定方法,由等腰三角形的三线合一性质得出AD⊥BC是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.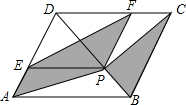 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )| A. | $\frac{3\sqrt{6}}{4}$ | B. | $\frac{3\sqrt{7}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{7}}{4}$ |
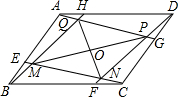 如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.
如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.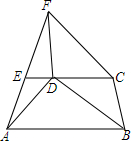 如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB.
如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB. 如图,在?ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求?ABCD的周长.
如图,在?ABCD中,E,F分别是AB、BC的中点,O是对角线的交点,若OE=4cm,OF=3cm,求?ABCD的周长.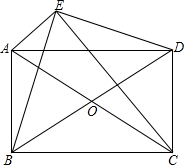 如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC,BD交于点O.
如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC,BD交于点O.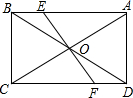 如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.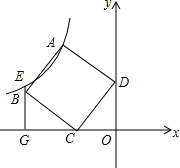 如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.