题目内容
14.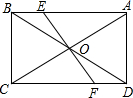 如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
分析 由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,则可证得△AOE≌△COF(ASA),继而证得OE=OF;可得EF=2OE=6.4,BE+CF=AB=10,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF;
∴CF=AE,OE=OF,
∵AB=10,BC=6,OE=3.2,
∴EF=2OE=6.4,AE+DF=BE+AE=AB=10,
∴四边形AEFD的周长为:AE+DF+BC+EF=6.4+10+6=22.4
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
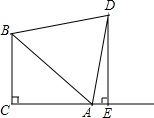 如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.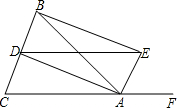 如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.
如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.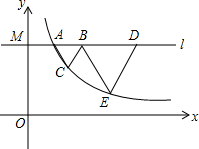 如图,过点M(0,3)的直线l平行于x轴,交反比例函数y=$\frac{k}{x}$的图象于点A,B、D是直线l上的点且满足$\frac{AB}{BD}$=$\frac{1}{2}$,以AB,BD为边向下作等边△ABC和等边△BDE,当C,E都落在y=$\frac{k}{x}$的图象上时,k=$\frac{6\sqrt{3}}{7}$.
如图,过点M(0,3)的直线l平行于x轴,交反比例函数y=$\frac{k}{x}$的图象于点A,B、D是直线l上的点且满足$\frac{AB}{BD}$=$\frac{1}{2}$,以AB,BD为边向下作等边△ABC和等边△BDE,当C,E都落在y=$\frac{k}{x}$的图象上时,k=$\frac{6\sqrt{3}}{7}$. 如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.
如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE. 如图,在?ABCD中,BD⊥AD,AD=8,AB=10,则AC的长为2$\sqrt{73}$.
如图,在?ABCD中,BD⊥AD,AD=8,AB=10,则AC的长为2$\sqrt{73}$.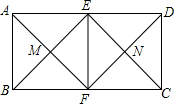 如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.
如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.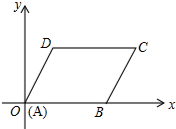 在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).
在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).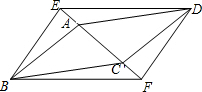 如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.
如图,?ABCD和?EBFD的顶点A,C,E,F在同一条直线上,求证:AE=CF.