题目内容
20.从⊙O外一点P引割线PBC,过P作直线PM,且∠OBC=∠CPM.(1)如图1,当PM与⊙O切于A点,且PA=2OB,求tan∠P的值;
(2)如图2,当PM交⊙O于E,D,且PE=2,ED=6,tan∠P=$\frac{2}{5}$,求⊙O的半径长.
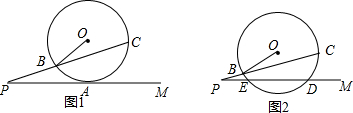
分析 (1)连接OA,OC,交PC于D,根据已知和等腰三角形的性质得出∠OCD=∠CPM,证得OC∥PM,根据切线的性质得出AO⊥OC,根据PA=2OB和平行线分线段成比例定理得出$\frac{OD}{AD}$=$\frac{OC}{PA}$=$\frac{OB}{PA}$=$\frac{1}{2}$,即可求得tan∠P的值;
(2)连接OC、OD,作OF⊥PM,则EF=FD=$\frac{1}{2}$ED=3,根据已知和等腰三角形的性质得出∠OCD=∠CPM,证得OC∥PM,根据切线的性质得出AO⊥OC,根据tan∠P=$\frac{2}{5}$,得出$\frac{GF}{PF}$=$\frac{2}{5}$,$\frac{OG}{OC}$=$\frac{2}{5}$,根据垂径定理求得PF,即可求得GF=2,设OF=x,则OG=x-2,得出$\frac{x-2}{\sqrt{{x}^{2}+9}}$=$\frac{2}{5}$,解方程求得x的值,然后根据勾股定理即可求得半径.
解答 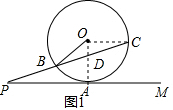 解:(1)连接OA,OC,
解:(1)连接OA,OC,
∵OB=OC,
∴∠OBC=∠OCD,
∵∠OBC=∠CPM,
∴∠OCD=∠CPM,
∴OC∥PM,
∵PM与⊙O切于A点,
∴OA⊥PA,
∴AO⊥OC,
∵OC∥PA,
∴$\frac{OD}{AD}$=$\frac{OC}{PA}$,
∵PA=2OB,OB=OC,
∴$\frac{OD}{AD}$=$\frac{1}{2}$,
∴$\frac{OD}{OA}$=$\frac{1}{3}$,
∴$\frac{OD}{OC}$=$\frac{1}{3}$,
∴tan∠OCD=$\frac{OD}{OC}$=$\frac{1}{3}$,
∵∠OCB=∠CPM,
∴tan∠P=$\frac{1}{3}$.
(2)连接OC、OD,作OF⊥PM,则EF=FD=$\frac{1}{2}$ED=3,
∴PF=PE+EF=2+3=5,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠OBC=∠CPM,
∴∠OCB=∠CPM,
∴OC∥PM,
∴OF⊥OC,
∵tan∠P=$\frac{2}{5}$,
∴$\frac{GF}{PF}$=$\frac{2}{5}$,
∴GF=2,
设OF=x,则OG=x-2,
在RT△OFD中,OD=$\sqrt{O{F}^{2}+D{F}^{2}}$=$\sqrt{{x}^{2}+{3}^{2}}$,
∴OC=$\sqrt{{x}^{2}+9}$,
∵tan∠P=$\frac{2}{5}$,∠OCB=∠CPM,
∴tan∠OCB=$\frac{OG}{OC}$=$\frac{2}{5}$,
∴$\frac{x-2}{\sqrt{{x}^{2}+9}}$=$\frac{2}{5}$,
∴5(x-2)=2$\sqrt{{x}^{2}+9}$,
两边平方,整理得,21x2-100x+64=0,
解得x1=4,x2=$\frac{16}{21}$<2(舍去),
∴OF=4,
在RT△OFD中,OD=$\sqrt{O{F}^{2}+F{D}^{2}}$=5,
∴⊙O的半径长为5.
点评 本题考查了切线的性质,等腰三角形的性质,平行线的判定和性质,勾股定理和直角三角形函数等,作出辅助线根据直角三角形是解题的关键.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案



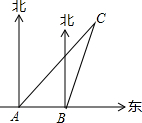 如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由. 如图,在△ABC中,DE⊥AB,DF⊥AC,垂足分别为点E,F,AE=AF,找出一对全等的三角形,并给出证明.
如图,在△ABC中,DE⊥AB,DF⊥AC,垂足分别为点E,F,AE=AF,找出一对全等的三角形,并给出证明.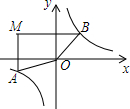 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为( )
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为( )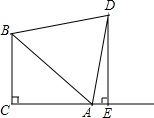 如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.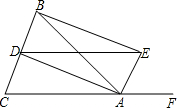 如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.
如图,△ABC中,AB=AC,AD,AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE,四边形AEBD是矩形吗?证明你的结论.