题目内容
13. 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
分析 先设D(a,b),得出CO=-a,CD=AB=b,k=ab,再根据△BCE的面积是6,得出BC×OE=12,最后根据AB∥OE,得出$\frac{BC}{OC}=\frac{AB}{EO}$,即BC•EO=AB•CO,求得ab的值即可.
解答 解:设D(a,b),则CO=-a,CD=AB=b,
∵矩形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=ab,
∵△BCE的面积是6,∴$\frac{1}{2}$×BC×OE=6,即BC×OE=12,
∵AB∥OE,
∴$\frac{BC}{OC}=\frac{AB}{EO}$,即BC•EO=AB•CO,
∴12=b×(-a),即ab=12,
∴k=12,
故选D.
点评 本题主要考查了反比例函数系数k的几何意义,矩形的性质以及平行线分线段成比例定理的综合应用,能很好地考核学生分析问题,解决问题的能力.解题的关键是将△BCE的面积与点D的坐标联系在一起,体现了数形结合的思想方法.

练习册系列答案
相关题目
3.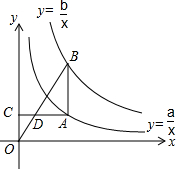 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
18.已知点A(a,2)与点B(3,b)关于x轴对称,则实数a,b的值是( )
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-2 | D. | a=-3,b=-2 |
12.甲、乙、丙三位同学参加“华罗庚杯数学竞赛”培训.三个培训段的考试成绩如表:
现要选拨一人参赛:
(1)若按三次平均成绩选拔,应选谁参加?
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
现要选拨一人参赛:
| 甲 | 乙 | 丙 | |
| 代数 | 85 | 85 | 70 |
| 几何 | 92 | 80 | 83 |
| 综合 | 75 | 85 | 90 |
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
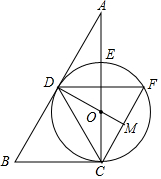 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.
如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.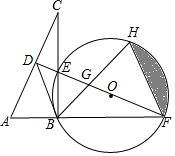 如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.
如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.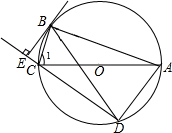 如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{AB}$=$\widehat{BD}$,BE⊥DC交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,$\widehat{AB}$=$\widehat{BD}$,BE⊥DC交DC的延长线于点E.