题目内容
12.甲、乙、丙三位同学参加“华罗庚杯数学竞赛”培训.三个培训段的考试成绩如表:现要选拨一人参赛:
| 甲 | 乙 | 丙 | |
| 代数 | 85 | 85 | 70 |
| 几何 | 92 | 80 | 83 |
| 综合 | 75 | 85 | 90 |
(2)若三次成绩按3:3:4的比例计算,应选谁参加?
(3)若三次成绩按20%,30%,50%计算,应选谁参加?
分析 (1)根据平均数的定义求出甲、乙、丙三位同学的平均数,进一步判定即可求解;
(2)三次成绩按3:3:4的比例计算求出加权平均数后判断即可;
(3)三次成绩按20%,30%,50%的比例计算求出加权平均数后判断即可.
解答 解:(1)(85+92+75)÷3=84,
(85+80+85)÷3=83$\frac{1}{3}$,
(70+83+90)÷3=81,
∵84>83$\frac{1}{3}$>81,
∴若按三次平均成绩选拔,应选甲参加;
(2)85×$\frac{3}{3+3+4}$+92×$\frac{3}{3+3+4}$+75×$\frac{4}{3+3+4}$
=25.5+27.6+30
=83.1,
85×$\frac{3}{3+3+4}$+80×$\frac{3}{3+3+4}$+85×$\frac{4}{3+3+4}$
=25.5+24+34
=83.5
70×$\frac{3}{3+3+4}$+83×$\frac{3}{3+3+4}$+90×$\frac{4}{3+3+4}$
=21+24.9+36
=81.9
∵83.5>83.1>81.9,
∴若三次成绩按3:3:4的比例计算,应选乙参加;
(3)85×20%+92×30%+75×50%
=17+27.6+37.5
=82.1,
85×20%+80×30%+85×50%
=17+24+42.5
=83.5
70×20%+83×30%+90×50%
=14+24.9+45
=83.9
∵83.9>83.5>82.1,
∴若三次成绩按20%,30%,50%计算,应选丙参加.
点评 考查了加权平均数,权的表现形式,一种是比的形式,另一种是百分比的形式,权的大小直接影响结果.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13. 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
17.下表是某种图书的册数与价格之间的关系,请根据表中数据解答下列问题:
(1)完成下表:
(2)根据表格可知价格(y)与册数(x)的函数解析式为y=7.5x,自变量的取值范围为x>0,且x为整数.
(3)画出函数图象.
(4)当售出6册时价格是多少元?
(1)完成下表:
| 册数(x) | 1 | 2 | 3 | … | |
| 价格(y) | 7.5 | 15 | 30 | … |
(3)画出函数图象.
(4)当售出6册时价格是多少元?
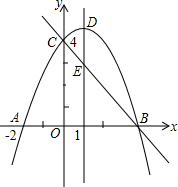 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.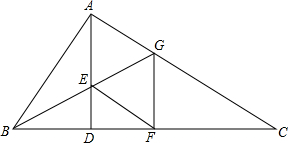 如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.
如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.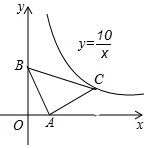 如图,在△ABC中,AB=AC,∠BAC=90°,点A在x轴上,点B的坐标是(0,3),若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,那么点C的坐标为(5,2).
如图,在△ABC中,AB=AC,∠BAC=90°,点A在x轴上,点B的坐标是(0,3),若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,那么点C的坐标为(5,2).