题目内容
1.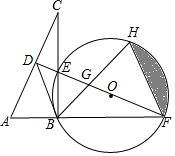 如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)求证:BD是⊙O的切线;
(2)当AB=BE=1时,求阴影部分的面积;
(3)在(2)的条件下,求$\frac{DB}{HF}$的值.
分析 (1)如图,连接OB,根据直角三角形斜边上的中线性质得DB=DC,则∠DBC=∠C,再根据等腰三角形的性质和对顶角相等得到∠OBE=∠OEB=∠CED,于是可得到∠DBC+∠OBE=90°,然后根据切线的判定方法可判定BD是⊙O的切线;
(2)连接AE、HO,如图,利用勾股定理计算出AE=$\sqrt{2}$,再利用线段垂直平分线性质得CE=AE=$\sqrt{2}$,所以BC=1+$\sqrt{2}$,接着证明△CAB≌△FEB得到BF=BC=1+$\sqrt{2}$,于是利用勾股定理可计算出EF2=4+2$\sqrt{2}$,然后根据扇形面积公式,利用S阴影=S扇形HOF-S△HOF进行计算即可;
(3)利用DB=$\frac{1}{2}$AC,AC=EF得到BD=$\frac{1}{2}$EF,利用△OFH为等腰直角三角形得到HF=$\sqrt{2}$OF,则HF=$\frac{\sqrt{2}}{2}$EF,于是可计算出$\frac{BD}{HF}$的值.
解答 (1)证明:如图,连接OB,
∵BD是Rt△ABC斜边上的中线,
∴DB=DC,
∴∠DBC=∠C,
∵OB=OE,
∴∠OBE=∠OEB=∠CED,
∵∠C+∠CED=90°,
∴∠DBC+∠OBE=90°,即∠DBO=90°,
∴OB⊥DB,
∴BD是⊙O的切线;
(2)解:连接AE、HO,如图,
∵AB=BE=1,
∴AE=$\sqrt{2}$,
∵DF垂直平分AC,
∴CE=AE=$\sqrt{2}$,
∴BC=1+$\sqrt{2}$,
∵∠C+∠CAB=90°,∠DFA+∠CAB=90°,
∴∠C=∠DFA,
在△CAB和△FEB中
$\left\{\begin{array}{l}{∠C=∠BFE}\\{∠ABC=∠EBF}\\{AB=EB}\end{array}\right.$
∴△CAB≌△FEB,
∴BF=BC=1+$\sqrt{2}$,
∴EF2=BE2+BF2=12+(1+$\sqrt{2}$)2=4+2$\sqrt{2}$,
∵BH平分∠CBF,
∴∠HBF=$\frac{1}{2}$∠EBF=45°,
∴∠HOF=2∠HBF=90°,
∴S阴影=S扇形HOF-S△HOF=$\frac{90•π•(\frac{EF}{2})^{2}}{360}$-$\frac{1}{2}$•($\frac{EF}{2}$)2=$\frac{(2+\sqrt{2})π}{8}$-$\frac{1}{2}$-$\frac{\sqrt{2}}{4}$;
(3)解:∵DB=$\frac{1}{2}$AC,
而AC=EF,
∴BD=$\frac{1}{2}$EF,
∵△OFH为等腰直角三角形,
∴HF=$\sqrt{2}$OF,
∴HF=$\frac{\sqrt{2}}{2}$EF,
∴$\frac{BD}{HF}$=$\frac{\frac{1}{2}EF}{\frac{\sqrt{2}}{2}EF}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了圆的综合题:熟练掌握线段垂直平分线的性质、直角三角形斜边上的中线性质、圆周角定理和切线的判定方法;会应用全等三角形的知识解决线段相等的问题;会利用规则面积的和差计算不规则图形的面积.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )



 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )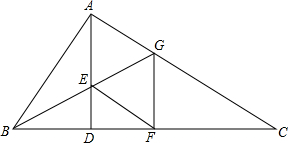 如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.
如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.