题目内容
4.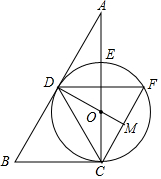 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.
如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.(1)求证:点M是CF的中点;
(2)若E是$\widehat{DF}$的中点,连结DF,DC,试判断△DCF的形状;
(3)在(2)的条件下,若BC=a,求AE的长.
分析 (1)根据垂径定理可知,只要证明OM⊥CF即可解决问题;
(2)结论:△DFC是等边三角形.由点M是CF中点,DM⊥CF,推出DE=DF,由E是$\widehat{DF}$中点,推出DC=CF,推出DC=CF=DF,即可;
(3)只要证明△BCD是等边三角形,即可推出∠B=60°,∠A=30°,在Rt△ABC中,BC=BD=CD=a,可得OC=OD=$\frac{\sqrt{3}}{3}$a,OA=$\frac{2\sqrt{3}}{3}$a,由此即可解决问题;
解答 (1)证明:∵AB是⊙O的切线,
∴OD⊥AB,
∴∠ODB=90°,
∵CF∥AB,
∴∠OMF=∠ODB=90°,
∴OM⊥CF,
∴CM=MF.
(2)解:结论:△DFC是等边三角形.
理由:∵点M是CF中点,DM⊥CF,
∴DE=DF,
∵E是$\widehat{DF}$中点,
∴DC=CF,
∴DC=CF=DF,
∴△DCF是等边三角形.
(3)解:∵BC、BD是切线,
∴BC=BD,
∵CE垂直平分DF,
∴∠DCA=30°,∠DCB=60°,
∴△BCD是等边三角形,
∴∠B=60°,∠A=30°,
在Rt△ABC中,BC=BD=CD=a,
∴OC=OD=$\frac{\sqrt{3}}{3}$a,OA=$\frac{2\sqrt{3}}{3}$a,
∴AE=OA-OC=$\frac{\sqrt{3}}{3}$a.
点评 本题考查切线的性质、等边三角形的判定和性质、垂径定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
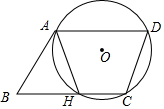 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H. 如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )



 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )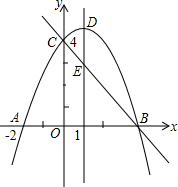 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.