题目内容
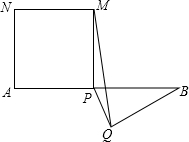 如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于
如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于考点:二次函数的最值,等腰三角形的性质,正方形的性质
专题:计算题
分析:设AP=x,则BP=4-x,MP=AP=x,Q点到MP的距离等于B点到MP的距离的一半,列出面积的表达式根据配方法即可求解.
解答:解:设AP=x,则BP=4-x,MP=AP=x,Q点到MP的距离等于B点到MP的距离的一半.
∵S△MPQ=
x•
=
(4x-x2)=
[4(x-2)2]≤1.
∴当x=2时,S△MPQ=1为最大值.
故答案为:1.
∵S△MPQ=
| 1 |
| 2 |
| 4-x |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴当x=2时,S△MPQ=1为最大值.
故答案为:1.
点评:本题考查了二次函数的最值及等腰三角形的性质,难度不大,关键是掌握用配方法求二次函数的最值.

练习册系列答案
相关题目

 如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是
如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是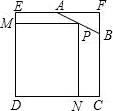 如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( ) 要挖一个面积为432m2的矩形养鱼池,周围两侧分别有宽为3m和4m的堤堰,如图所示,要想占地总面积最少,问水池的长与宽应为多少?
要挖一个面积为432m2的矩形养鱼池,周围两侧分别有宽为3m和4m的堤堰,如图所示,要想占地总面积最少,问水池的长与宽应为多少?