题目内容
若x2+y2+
=2x+y,那么xy+yx= .
| 5 |
| 4 |
考点:完全平方公式
专题:
分析:首先将原式移项配方,可得:∴(x-1)2+(y-
)2=0,由非负数的和为零,则每个为零的性质,即可求得x与y的值,则问题得解.
| 1 |
| 2 |
解答:解:∵x2+y2+
=2x+y,
∴x2+y2+
-2x-y=0,
∴(x-1)2+(y-
)2=0,
∴x-1=0,y-
=0,
∴x=1,y=
,
∴xy+yx=1+
=
.
故答案为:
.
| 5 |
| 4 |
∴x2+y2+
| 5 |
| 4 |
∴(x-1)2+(y-
| 1 |
| 2 |
∴x-1=0,y-
| 1 |
| 2 |
∴x=1,y=
| 1 |
| 2 |
∴xy+yx=1+
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:此题考查了配方法与非负数的和为零,则每个为零的性质.解题的关键是要注意分析.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知实数x满足条件x>
x+1,那么
+
的值等于( )
| 2 |
| (x+2)2 |
| 3 | (x-3)3 |
| A、2x-1 | B、-2x+1 |
| C、-5 | D、1 |
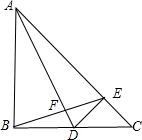 已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.
已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.