题目内容
15.已知$\left\{\begin{array}{l}{4x-3y=6z}\\{x+2y=7z}\end{array}\right.$,则代数式$\frac{x+5y+7z}{2x+3y+6z}$的值为$\frac{10}{9}$.分析 把方程组$\left\{\begin{array}{l}{4x-3y=6z①}\\{x+2y=7z②}\end{array}\right.$看作关于x和y的二元一次方程组,利用加减消元法得到y=2x,再利用代入法可得到x=3z,然后把x=3z,y=2z代入代数式中进行分式的计算即可.
解答 解:$\left\{\begin{array}{l}{4x-3y=6z①}\\{x+2y=7z②}\end{array}\right.$,
②×4-①的得8y+3y=28z-6z,
解得y=2z,
把y=2z代入②得x+4z=7z,
解得x=3z,
所以原式=$\frac{3z+10z+7z}{6z+6z+6z}$=$\frac{10}{9}$.
故答案为$\frac{10}{9}$.
点评 本题考查了解三元一次方程组:利用代入消元法或加减消元法把解三元一次方程组的问题转化为解二元一次方程组的问题.也考查了求分式的值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3.若x-|x|=0,则$\sqrt{{x}^{2}}$=( )
| A. | x | B. | -|x| | C. | -x | D. | x2 |
 如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系.
如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系. 如图,在△ABC中,∠ABC=48°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则∠ADC=66°.
如图,在△ABC中,∠ABC=48°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则∠ADC=66°.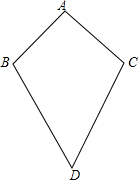 如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.
如图,在筝形四边形ABDC中,AB=AC,BD=CD,已知∠BAC=80°,∠BDC=60°,试求∠B的大小.