题目内容

20．设a，b，c都是非负数，且满足a+b+c=3，3a+b-c=5，则5a+4b+2c的最大值是13．

分析 把c看作常数，解出b、c，代入所求式子即可解决问题．

解答 解：由$\left\{\begin{array}{l}{a+b+c=3}\\{3a+b-c=5}\end{array}\right.$解得$\left\{\begin{array}{l}{b=4-2a}\\{c=a-1}\end{array}\right.$，
所以5a+4b+2c=5a+16-8a+2a-=14-a，
∴a是非负数，∴a≥1
∴5a+4b+2c=14-a的最大值为13．
故答案为13．

点评 本题考查一次函数的性质、方程组等知识，解题的关键是利用解方程组的思想解决问题，属于中考常考题型．

练习册系列答案
相关题目
10．已知x=$\sqrt{5}$+2，y=$\sqrt{5}$-2，则x2+2xy+y2的值是20．
11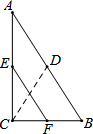．如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点，则DC和EF的大小关系是（　　）
A．DC＞EFB．DC＜EFC．DC=EFD．无法比较
8．来自某综合商场财务部的报告表明，商场1-5月份的销售总额一共是370万元，图1、图2反映的是商场今年1-5月份的商品销售额统计情况．
（1）该商场三月份销售总额是60万元．
（2）试求四月份的销售总额，并求服装部四月份销售额占1-5月份销售总额的百分比（结果百分比中保留两位小数）．
（3）有人认为5月份服装部月销售额比4月份减少了，你认为正确吗？请说明理由．
15．小张参加某节目的海选，共有17位选手参加决逐争取8个晋级名额，已知他们的分数互不相同，小张要判断自己是否能够晋级，只要知道17名选手成绩统计量中的（　　）
A．众数B．方差C．中位数D．平均数
5．下列运算正确的是（　　）
A．a•a2=a2B．（ab）2=ab2C．a6÷a2=a4D．（a2）3=a5
12．下列一元二次方程有两个相等的实数根的是（　　）
A．x2+1=0B．x2+4x+4=0C．x2+x+（-$\frac{1}{2}$）=0D．x2-x+$\frac{1}{2}$=0
9．已知x、y满足方程组$\left\{\begin{array}{l}{x+5y=12}\\{3x-y=4}\end{array}\right.$，则x+y的值为（　　）
A．-2B．2C．-4D．4
18．下列式子中，错误的是（　　）
A．$\sqrt{2}$×$\sqrt{8}$=4B．$\sqrt{（-4）×（-9）}$=$\sqrt{-4}$×$\sqrt{-9}$C．$\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$D．$\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网