题目内容
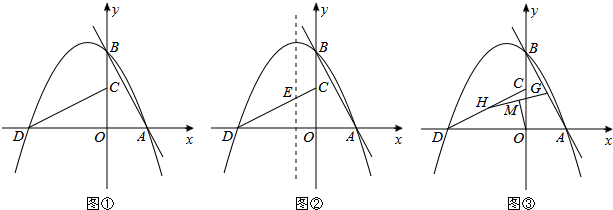
如图①,直线l:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=-2x+2,则P表示的函数解析式为 ;若P:y=-x2-3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=-2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx-4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=
,直接写出l,P表示的函数解析式.
(1)若l:y=-2x+2,则P表示的函数解析式为
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=-2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx-4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=
| 10 |

考点:二次函数综合题,一次函数的应用,勾股定理,等腰直角三角形,平行四边形的性质,作图-旋转变换
专题:压轴题,新定义
分析:(1)若l:y=-2x+2,求出点A、B、D的坐标,利用待定系数法求出P表示的函数解析式;若P:y=-x2-3x+4,求出点D、A、B的坐标,再利用待定系数法求出l表示的函数解析式;
(2)根据对称轴的定义解答即可;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标.注意:点Q的坐标有两个,如答图1所示,不要漏解;
(4)如答图2所示,作辅助线,构造等腰直角三角形OGH,求出OG的长度,进而由AB=2OG求出AB的长度,再利用勾股定理求出y=mx-4m中m的值,最后分别求出l,P表示的函数解析式.
(2)根据对称轴的定义解答即可;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标.注意:点Q的坐标有两个,如答图1所示,不要漏解;
(4)如答图2所示,作辅助线,构造等腰直角三角形OGH,求出OG的长度,进而由AB=2OG求出AB的长度,再利用勾股定理求出y=mx-4m中m的值,最后分别求出l,P表示的函数解析式.
解答:解:(1)若l:y=-2x+2,则A(1,0),B(0,2).
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴D(-2,0).
设P表示的函数解析式为:y=ax2+bx+c,将点A、B、D坐标代入得:
,
解得
,
∴P表示的函数解析式为:y=-x2-x+2;
若P:y=-x2-3x+4=-(x+4)(x-1),
则D(-4,0),A(1,0).
∴B(0,4).
设l表示的函数解析式为:y=kx+b,将点A、B坐标代入得:
,解得
,
∴l表示的函数解析式为:y=-4x+4.
(2)直线l:y=mx+n(m>0,n<0),
令y=0,即mx+n=0,得x=-
;
令x=0,得y=n.
∴A(-
,0)、B(0,n),
∴D(-n,0).
设抛物线对称轴与x轴的交点为N(x,0),
∵DN=AN,
∴-
-x=x-(-n),
∴2x=-n-
,
∴P的对称轴为x=-
.
(3)若l:y=-2x+4,则A(2,0)、B(0,4),
∴C(0,2)、D(-4,0).
可求得直线CD的解析式为:y=
x+2.
由(2)可知,P的对称轴为x=-1.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y=
x+b.
∵点E、点C的横坐标相差1,
∴点F、点Q的横坐标也是相差1.
则|xF-(-1)|=|xF+1|=1,
解得xF=0或xF=-2.
∵点F在直线ll:y=-2x+4上,
∴点F坐标为(0,4)或(-2,8).
若F(0,4),则直线FQ的解析式为:y=
x+4,
当x=-1时,y=
,
∴Q1(-1,
);
若F(-2,8),则直线FQ的解析式为:y=
x+9,
当x=-1时,y=
,
∴Q2(-1,
).
∴满足条件的点Q有2个,如答图1所示,点Q坐标为Q1(-1,
)、Q2(-1,
).
(4)如答图2所示,连接OG、OH.
∵点G、H为斜边中点,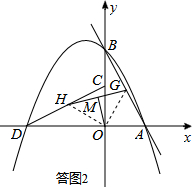
∴OG=
AB,OH=
CD.
由旋转性质可知,AB=CD,OG⊥OH,
∴△OGH为等腰直角三角形.
∵点G为GH中点,
∴△OMG为等腰直角三角形,
∴OG=
OM=
•
=2
,
∴AB=2OG=4
.
∵l:y=mx-4m,
∴A(4,0),B(0,-4m).
在Rt△AOB中,由勾股定理得:OA2+OB2=AB2,
即:42+(-4m)2=(4
)2,
解得:m=-2或m=2,
∵点B在y轴正半轴,
∴m=2舍去,∴m=-2.
∴l表示的函数解析式为:y=-2x+8;
∴B(0,8),D(-8,0).
又A(4,0),
利用待定系数法求得P:y=-
x2-x+8.
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴D(-2,0).
设P表示的函数解析式为:y=ax2+bx+c,将点A、B、D坐标代入得:
|
解得
|
∴P表示的函数解析式为:y=-x2-x+2;
若P:y=-x2-3x+4=-(x+4)(x-1),
则D(-4,0),A(1,0).
∴B(0,4).
设l表示的函数解析式为:y=kx+b,将点A、B坐标代入得:
|
|
∴l表示的函数解析式为:y=-4x+4.
(2)直线l:y=mx+n(m>0,n<0),
令y=0,即mx+n=0,得x=-
| n |
| m |
令x=0,得y=n.
∴A(-
| n |
| m |
∴D(-n,0).
设抛物线对称轴与x轴的交点为N(x,0),
∵DN=AN,
∴-
| n |
| m |
∴2x=-n-
| n |
| m |
∴P的对称轴为x=-
| mn+n |
| 2m |

(3)若l:y=-2x+4,则A(2,0)、B(0,4),
∴C(0,2)、D(-4,0).
可求得直线CD的解析式为:y=
| 1 |
| 2 |
由(2)可知,P的对称轴为x=-1.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y=
| 1 |
| 2 |
∵点E、点C的横坐标相差1,
∴点F、点Q的横坐标也是相差1.
则|xF-(-1)|=|xF+1|=1,
解得xF=0或xF=-2.
∵点F在直线ll:y=-2x+4上,
∴点F坐标为(0,4)或(-2,8).
若F(0,4),则直线FQ的解析式为:y=
| 1 |
| 2 |
当x=-1时,y=
| 7 |
| 2 |
∴Q1(-1,
| 7 |
| 2 |
若F(-2,8),则直线FQ的解析式为:y=
| 1 |
| 2 |
当x=-1时,y=
| 17 |
| 2 |
∴Q2(-1,
| 17 |
| 2 |
∴满足条件的点Q有2个,如答图1所示,点Q坐标为Q1(-1,
| 7 |
| 2 |
| 17 |
| 2 |
(4)如答图2所示,连接OG、OH.
∵点G、H为斜边中点,

∴OG=
| 1 |
| 2 |
| 1 |
| 2 |
由旋转性质可知,AB=CD,OG⊥OH,
∴△OGH为等腰直角三角形.
∵点G为GH中点,
∴△OMG为等腰直角三角形,
∴OG=
| 2 |
| 2 |
| 10 |
| 5 |
∴AB=2OG=4
| 5 |
∵l:y=mx-4m,
∴A(4,0),B(0,-4m).
在Rt△AOB中,由勾股定理得:OA2+OB2=AB2,
即:42+(-4m)2=(4
| 5 |
解得:m=-2或m=2,
∵点B在y轴正半轴,
∴m=2舍去,∴m=-2.
∴l表示的函数解析式为:y=-2x+8;
∴B(0,8),D(-8,0).
又A(4,0),
利用待定系数法求得P:y=-
| 1 |
| 4 |
点评:本题是二次函数压轴题,综合考查了二次函数的图象与性质、一次函数、待定系数法、旋转变换、平行四边形、等腰直角三角形、勾股定理等多个知识点,综合性较强,有一定的难度.题干中定义了“关联抛物线”与“关联直线”的新概念,理解这两个概念是正确解题的前提.

练习册系列答案
相关题目
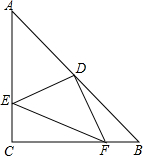 如图,在△ABC中,AC=BC,∠C=90°,D为AB边的中点,点E在AC上,连接DE,过D作DF⊥DE交BC于F.若AE=6cm,BF=2cm,则ED的长为( )
如图,在△ABC中,AC=BC,∠C=90°,D为AB边的中点,点E在AC上,连接DE,过D作DF⊥DE交BC于F.若AE=6cm,BF=2cm,则ED的长为( )A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,则BC的长为( )
| A、8cm | B、7cm |
| C、6cm | D、5cm |
若9a2+6(k-3)a+1是完全平方式,则k的值是( )
| A、±4 | B、±2 | C、3 | D、4或2 |
 如图,直线l1:y=-
如图,直线l1:y=- 已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.
已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.