��Ŀ����
��ѧ���ϣ�����ʦ��ʾ������1����ͼ1���ı���ABCD�������Σ�BC=2���Խ��߽������O����E�DZ�BC�ӳ�����һ�㣮����OE��CD����F����CE=x��CF=y����y����x�ĺ�������ʽ���䶨����
��1������˼����С����Ϊ����ͨ�����Ӹ�����--����O��OM��BC������ΪM��⣮����Ϊ����뷨��������д������1�Ĵ𰸼���Ӧ���Ƶ����̣�
��2�����������1�е��������ı���ABCD�������Σ�BC=2����Ϊ���ı���ABCD��ƽ���ı��Σ�BC=3��CD=2���������������䣨��ͼ2������ֱ��д�������ı��ĺ�������ʽ��
��3�����������1�е��������ı���ABCD�������Σ�BC=2����һ����Ϊ�����ı���ABCD�����Σ�AD��BC��BC=4��CD=3��AD=2�������������䣨��ͼ3��������д�������ٴθı��y����x�ĺ�������ʽ�Լ���Ӧ���Ƶ����̣�

��1������˼����С����Ϊ����ͨ�����Ӹ�����--����O��OM��BC������ΪM��⣮����Ϊ����뷨��������д������1�Ĵ𰸼���Ӧ���Ƶ����̣�
��2�����������1�е��������ı���ABCD�������Σ�BC=2����Ϊ���ı���ABCD��ƽ���ı��Σ�BC=3��CD=2���������������䣨��ͼ2������ֱ��д�������ı��ĺ�������ʽ��
��3�����������1�е��������ı���ABCD�������Σ�BC=2����һ����Ϊ�����ı���ABCD�����Σ�AD��BC��BC=4��CD=3��AD=2�������������䣨��ͼ3��������д�������ٴθı��y����x�ĺ�������ʽ�Լ���Ӧ���Ƶ����̣�
���㣺�ı����ۺ���
ר�⣺
��������1�����������ε����ʵ�OB=OD����֪OM��DC�����OM��CM�ij����ٸ���ƽ���߷��߶γɱ����������ɵý⣻
��2������ƽ���ı��ε����ʵ�OB=OD����OM��CD�����OM��CM�ij����ٸ���ƽ���߷��߶γɱ����������ɵý⣻
��3��AD��BC��
=
=
��
=
=
=
������O��ON��CD����BC�ڵ�N����ƽ���߷��߶γɱ����������ON=2��BN=
��CN=4-
=
������EN=x+
������
=
�������y����x�ĺ�������ʽ��
��2������ƽ���ı��ε����ʵ�OB=OD����OM��CD�����OM��CM�ij����ٸ���ƽ���߷��߶γɱ����������ɵý⣻
��3��AD��BC��
| BO |
| OD |
| BC |
| AD |
| 4 |
| 2 |
| BO |
| BD |
| 4 |
| 4+2 |
| 4 |
| 6 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| CF |
| ON |
| CE |
| EN |
����⣺��1������O��OM��BC������ΪM��
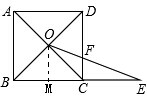
���ı���ABCD�������Σ�
��OB=OD��
��OM��BC��
���OMB=��DCB=90�㣬
��OM��DC��
��OM=
DC=1��CM=
BC=1��
��OM��DC��
��
=
��
��
=
��
���y=
��������Ϊx��0��
��2����OM��CD����CD�ڵ�M��
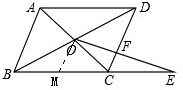
���ı���ABCD��ƽ���ı����Σ�
��OB=OD��
��OM��CD��
��OM=
DC=1��CM=
BC=
��
��OM��DC��
��
=
��
��
=
�����y=
��������Ϊx��0��
��3��AD��BC��
=
=
��
=
=
=
��
����O��ON��CD����BC�ڵ�N��
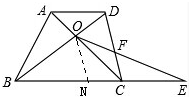
��
=
��
��ON=2��
��ON��CD��
=
=
��
��BN=
��
��CN=4-
=
��
��EN=x+
��
��ON��CD��
��
=
����
=
��
��y=
��y����x�ĺ�������ʽΪy=
��x��0����

���ı���ABCD�������Σ�
��OB=OD��
��OM��BC��
���OMB=��DCB=90�㣬
��OM��DC��
��OM=
| 1 |
| 2 |
| 1 |
| 2 |
��OM��DC��
��
| CF |
| OM |
| CE |
| EM |
��
| y |
| 1 |
| x |
| x+1 |
���y=
| x |
| x+1 |
��2����OM��CD����CD�ڵ�M��

���ı���ABCD��ƽ���ı����Σ�
��OB=OD��
��OM��CD��
��OM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��OM��DC��
��
| CF |
| OM |
| CE |
| EM |
��
| y |
| 1 |
| x | ||
x+
|
| 2x |
| 2x+3 |
��3��AD��BC��
| BO |
| OD |
| BC |
| AD |
| 4 |
| 2 |
| BO |
| BD |
| 4 |
| 4+2 |
| 4 |
| 6 |
| 2 |
| 3 |
����O��ON��CD����BC�ڵ�N��

��
| ON |
| DC |
| BO |
| BD |
��ON=2��
��ON��CD��
| BN |
| BC |
| ON |
| CD |
| 2 |
| 3 |
��BN=
| 8 |
| 3 |
��CN=4-
| 8 |
| 3 |
| 4 |
| 3 |
��EN=x+
| 4 |
| 3 |
��ON��CD��
��
| CF |
| ON |
| CE |
| EN |
| y |
| 2 |
| x | ||
x+
|
��y=
| 6x |
| 3x+4 |
��y����x�ĺ�������ʽΪy=
| 6x |
| 3x+4 |
������������Ҫ�������ı��ε��ۺ�Ӧ�ã��õ������Ρ�ƽ���ı��Ρ����ε������Լ�ƽ���߷��߶γɱ����������ѶȽϴ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
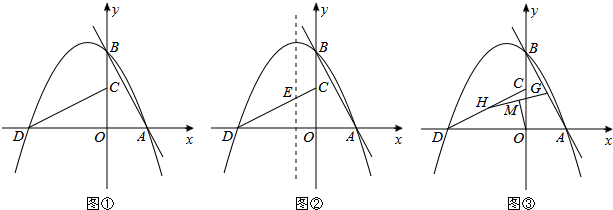
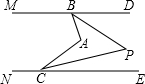 ��ͼ����֪����MBA+��BAC+��NCA=360�㣬
��ͼ����֪����MBA+��BAC+��NCA=360�㣬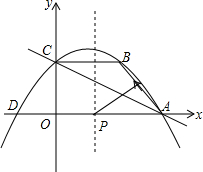 ��ͼ��ֱ��y=-
��ͼ��ֱ��y=-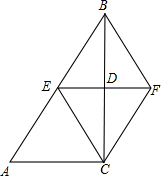 ��ͼ���ڡ�ABC�У���ACB=90�㣬BC�Ĵ�ֱƽ����EF��BC�ڵ�D����AB�ڵ�E����BE=BF������һ����������֤���ı���BECFΪ�����ε���
��ͼ���ڡ�ABC�У���ACB=90�㣬BC�Ĵ�ֱƽ����EF��BC�ڵ�D����AB�ڵ�E����BE=BF������һ����������֤���ı���BECFΪ�����ε���