题目内容
在Rt△ABC中，∠C=90°，AB=10cm，AC=6cm，则BC的长为（ ）
| A、8cm | B、7cm |
| C、6cm | D、5cm |
考点：勾股定理
专题：
分析：利用勾股定理：直角三角形中两条直角边的平方和等于斜边的平方解题即可．
解答：解：∵∠C=90°，AB=10cm，AC=6cm，
∴BC=
=8cm，
故选A．
∴BC=
| 102-62 |
故选A．
点评：本题考查了勾股定理的知识，属于基础题目，像这类直接考查定义的题目，解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式．
练习册系列答案
名校课堂系列答案
相关题目
下列方程中，解为2的是（ ）
| A、2x=6 |
| B、5x-8=2 |
| C、-x-2=0 |
| D、x+2=3x |
计算2001×1999+0.25×4的值是（ ）
| A、2×104 |
| B、4×105 |
| C、4×106 |
| D、2×107 |
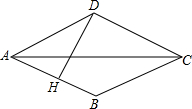如图，菱形ABCD的边长为15cm，对角线AC=24cm，DH⊥AB于H，则DH的长为（ ）| A、14.4cm |
| B、16.2cm |
| C、15.4cm |
| D、18.2cm |
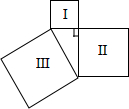如图，有3个正方形，已知第Ⅰ和第Ⅱ个正方形的边长分别为5cm和10cm，则第Ⅲ个正方形的周长为（ ）A、20
| ||
B、25
| ||
C、20
| ||
D、25
|
在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，且满足∠A：∠B：∠C=1：2：3，则△ABC一定是（ ）
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不能确定 |
如图，下列条件能判断AD∥CB的是（ ）| A、∠D+∠DAB=180° |
| B、∠1=∠2 |
| C、∠3=∠4 |
| D、∠4=∠5 |
