题目内容
 已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.
已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:利用平行四边形的性质得出∠DAE=∠BCF,AD=BC,∠D=∠B,进而结合平行线的性质和全等三角形的判定方法得出答案.
解答:证明:∵?ABCD,∴AD=BC,∠D=∠B,∠DAB=∠DCB,
又 AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
,
∴△DAE≌△BCF(ASA),
∴AE=CF.
又 AE平分∠BAD,CF平分∠BCD,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
|
∴△DAE≌△BCF(ASA),
∴AE=CF.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定等知识,得出∠DAE=∠BCF是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
下列说法中,错误的是( )
| A、“同位角相等”是命题 |
| B、证明假命题,只要举一个反例即可 |
| C、命题是判断一件事情的句子 |
| D、任意两个正方形都是位似图形 |
在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且满足∠A:∠B:∠C=1:2:3,则△ABC一定是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不能确定 |
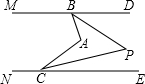 如图,已知,∠MBA+∠BAC+∠NCA=360°,
如图,已知,∠MBA+∠BAC+∠NCA=360°,